У практиці часто використовуються функції і т. д., тобто функція вигляду , де - задане число, - змінна. Такі функції називають показниковими. Ця назва пояснюється тим, що аргументом показникової функції є показник степеня, а основою степеня - задане число.
Функція, задана формулою (де ), називається показниковою функцією з основою .
Сформулюємо основні властивості показникової функції.
1. Область визначення — множина дійсних чисел.
2. Область значень — множина всіх додатних дійсних чисел.
3. При функція зростає на всій числовій прямій; при функція спадає на множині .
, якщо ,
, якщо
4. При будь-яких дійсних значеннях і справедливі рівності
Графіки показникових функцій зображені на малюнках:
1) для випадку
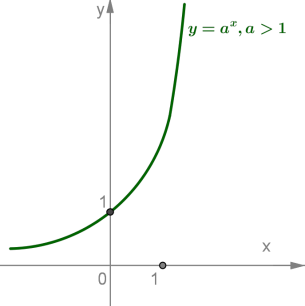
2) для випадку
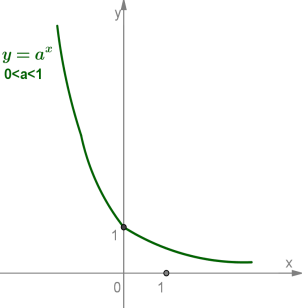
Побудуємо графіки функцій і , використавши розглянуті властивості і знайшовши кілька точок, що належать графіку.
Приклад:
Відзначимо, що графік функції проходить через точку і розташований вище осі
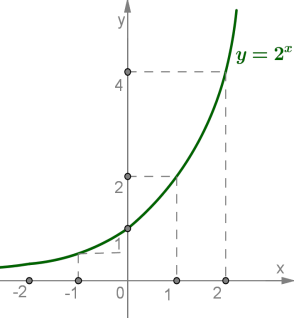
Якщо і спадає, тоді графік швидко наближається до осі (але не перетинає її);
якщо і зростає, тоді графік швидко піднімається вгору.
Такий вигляд має графік будь-якої функції , якщо
Приклад:
Графік функції також проходить через точку і розташований вище осі
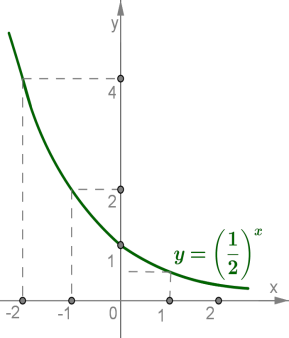
Якщо і зростає, тоді графік швидко наближається до осі (не перетинаючи її);
якщо і спадає, тоді графік швидко піднімається вгору.
Такий же вигляд має графік будь-якої функції , якщо .
Поазникові функції займають певну роль у житті людини. Наприклад, вони є математичними моделями таких процесів: зміна популяції протягом певного часу; зміна радіоактивності з плином часу.