Системи показникових і логарифмічних нерівностей — урок. Алгебра, 11 клас.

Умова, за якою треба знайти множину спільних розв'язків двох або декількох нерівностей із двома або більше змінними, називається системою нерівностей.

Розв'язати систему нерівностей — означає знайти множину всіх спільних для всіх нерівностей розв'язків.

Розв'язком системи нерівностей називається значення змінної, яке кожну з нерівностей системи перетворює на правильну числову нерівність.

Щоб знайти розв'язок системи нерівностей, потрібно знайти перетин множин розв’язків нерівностей, що входять до неї.

Приклад:

Розв'яжи систему нерівностей:

\{\begin{cases} 7^{2 x + 1} > 49 \\ 2 x - 4 > 3 \end{cases}

Розв'язання

Представимо \(49\) у вигляді степеня з основою \(7\) у першій нерівності:

\{\begin{cases} 7^{2 x + 1} > 7^{2} \\ 2 x - 4 > 3 \end{cases} \Rightarrow \{\begin{cases} 2 x + 1 > 2 \\ 2x - 4 > 3 \end{cases}

Оскільки

y = 7^{t}, (7 > 1)

— зростаюча функція, то знак нерівності не змінюється.

\{\begin{cases} 2 x > 2 - 1 \\ 2 x > 3 + 4 \end{cases} \Rightarrow \{\begin{cases} 2 x > 1 | : 2 \\ 2 x > 7 | : 2 \end{cases} \Rightarrow \{\begin{cases} x > 0,5 \\ x > 3,5 \end{cases}

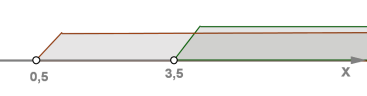
Відповідь:

x \in (3,5; + \infty)

Приклад:

Розв'яжи систему нерівностей:

\{\begin{cases} \log_{\frac{1}{3}} (5 x - 1) \geq 0 \\ 2 x + 4 > 3 \end{cases}

Розв'язання

\(1.\) У першій нерівності запишемо \(0\) у вигляді логарифма з основою

\frac{1}{3}

\(.\)

\{\begin{cases} \log_{\frac{1}{3}} (5 x - 1) \geq \log_{\frac{1}{3}} 1 \\ 2 x + 4 > 3 \end{cases} \Rightarrow \{\begin{cases} 5 x - 1 \leq 1 \\ 2 x + 4 > 3 \end{cases}

Оскільки

y = \log_{\frac{1}{3}} t

— спадна

(0 < \frac{1}{3} < 1)

\(,\) знак нерівності змінюється.

\{\begin{cases} 5 x \leq 1 + 1 \\ 2 x > 3 - 4 \end{cases} \Rightarrow \{\begin{cases} 5 x \leq 2 | : 5 \\ 2 x > - 1 | : 2 \end{cases} \Rightarrow \{\begin{cases} x \leq 0, 4 \\ x > - 0,5 \end{cases}

x \in (- 0,5; 0, 4]

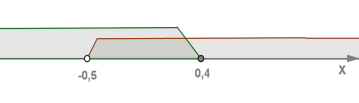
\(2.\) \(ОДЗ.\) Вираз під знаком логарифма має бути додатним.

\begin{array}{l} 5 x - 1 > 0 \\ 5 x > 1 | : 5 \\ x > 0,2 \\ x \in (0,2; + \infty) \end{array}

\(3.\) Перевіримо належність множини розв'язків системи \(ОДЗ\)\(:\)

\{\begin{cases} x \in (- 0,5; 0, 4] \\ x \in (0,2; + \infty) \end{cases}

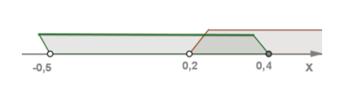
Відповідь:

x \in (0,2; 0, 4]

Попередня тема

Повернутись до теми

Наступне завдання

Відправити відгук

Знайшли помилку?

Розкажіть нам!