Для позначення числами точного положення точки на площині проведемо дві перпендикулярні координатні прямі \(x\) та \(y\), які перетинаються на початку відліку — у точці \(O\). Тим самим на площині задана прямокутна система координат, яка перетворює звичайну площину в координатну.
Точку \(O\) називають початком координат, координатні прямі \(x\) та \(y\) називають осями координат, а прямі кути, утворені осями координат, називають координатною чвертю. Координатні чверті пронумеровані так:
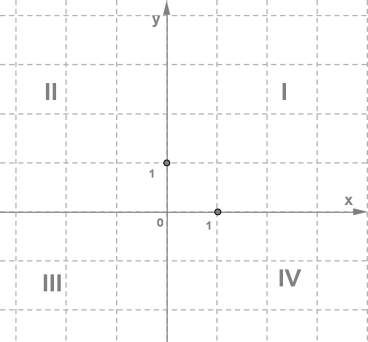
Зобразимо прямокутну систему координат і відзначимо в ній точку \(M\).

Проведемо через точку \(M\) пряму, паралельну осі \(y\).
Пряма перетне вісь \(x\) у деякій точці, координата якої дорівнює \(-2\).
Цю координату називають абсцисою точки \(M\).
Пряма перетне вісь \(x\) у деякій точці, координата якої дорівнює \(-2\).
Цю координату називають абсцисою точки \(M\).
Далі проведемо через точку \(M\) пряму, паралельну осі \(x\). Пряма перетинає вісь \(y\) у деякій точці, координата якої дорівнює \(3\).
Цю координату називають ординатою точки \(M\).
Цю координату називають ординатою точки \(M\).
Коротко пишемо так: \(M (x; y)\)
Цю пару чисел називають координатами точки \(M\).
Абсцису записуємо на перше місце, ординату — на друге місце.
Цю пару чисел називають координатами точки \(M\).
Абсцису записуємо на перше місце, ординату — на друге місце.
Маємо \(M (-2, 3)\).
Число \(-2\) називають абсцисою точки \(M\), а число \(3\) — ординатою точки \(M\).
Число \(-2\) називають абсцисою точки \(M\), а число \(3\) — ординатою точки \(M\).
Горизонтальну координатну пряму \(x\) називають віссю абсцис або віссю \(x\), а
вертикальну координатну пряму \(y\) — віссю ординат або віссю \(y\).
вертикальну координатну пряму \(y\) — віссю ординат або віссю \(y\).
Якщо точка \(M (x; y)\) належить першій координатній чверті, тоді \(x> 0; y> 0\);
якщо точка \(M (x; y)\) належить другій координатній чверті, тоді \(x <0; y> 0\);
якщо точка \(M (x; y)\) належить третій координатній чверті, тоді \(x <0; y <0\);
якщо точка \(M (x; y)\) належить четвертій координатній чверті, тоді \(x> 0; y <0\).
якщо точка \(M (x; y)\) належить другій координатній чверті, тоді \(x <0; y> 0\);
якщо точка \(M (x; y)\) належить третій координатній чверті, тоді \(x <0; y <0\);
якщо точка \(M (x; y)\) належить четвертій координатній чверті, тоді \(x> 0; y <0\).
Якщо точка \(M\) знаходиться на осі \(x\), то вона має координати \((x; 0)\), а якщо перебуває на осі \(y\), то вона має координати \((0; y)\).
Кожній точці на координатній площині відповідає пара чисел: її абсциса і ордината, і навпаки, кожній парі чисел відповідає одна точка площини, для якої ці числа є координатами.
Для побудови точки \(M (a; b)\)., потрібно знайти точку перетину прямих \(x = a\) та \(y = b\).
Це й буде шукана точка
Це й буде шукана точка