Розглянемо квадрат. Якщо відома сторона квадрата, то легко можна обчислити значення його площі:
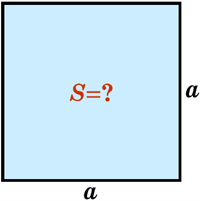
\(S=a^2.\)
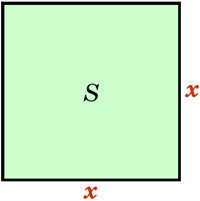
Однак, часто доводиться розв’язувати й обернену задачу: за відомою площею квадрата треба знайти довжину його сторони.
Приклад:
Площа квадрата дорівнює \(25\) \( см^2\). Знайди довжину сторони квадрата.
Розв’язання
Нехай сторона квадрата дорівнює \(x\) \(см.\) Тоді площа цього квадрата дорівнюватиме \(x^2\) \(см^2.\)
Маємо рівняння: \(x^2=25.\)
Це рівняння має два корені: \(5\) і \(-5\). Справді, \(5^2=25\) і \((-5)^2=25.\)
Оскільки довжина сторони квадрата не може бути від’ємним числом, то умову задачі задовольняє лише перший корінь рівняння — число \(5.\) Отже, довжина сторони квадрата дорівнює \(5\) \(см.\)
Відповідь: \(5\) \(см.\)
Корені рівняння \(x^2=25\), тобто числа, квадрати яких дорівнюють \(25\), називають квадратними коренями із числа \(25\).
Квадратним коренем із числа \(a\) називають число, квадрат якого дорівнює \(a\).
Приклад:
Квадратними коренями із числа \(49\) є числа \(7\) і \(-7\), бо \(7^2=49\) і \((-7)^2=49.\)
Квадратними коренями із числа \(100\) є числа \(10\) і \(-10\), бо \(10^2=100\) і \((-10)^2=100.\)
Квадратним коренем із числа \(0\) є лише одне число — число \(0\), бо \(0^2=0.\)
Однак, квадратного кореня із числа \(-9\) ми не знайдемо, оскільки серед відомих нам чисел не існує такого числа, квадрат якого дорівнював би \(-9.\)
Отже, не існує числа, квадрат якого дорівнює від’ємному числу.
Квадратного кореня з від’ємного числа не існує.