Числові вирази складаються з чисел за допомогою знаків арифметичних дій і дужок.
Число, яке ми отримуємо в результаті виконання дій у числовому виразі, називають значенням виразу.
Зверни увагу!
Якщо у виразі зустрічається ділення на нуль, то цей вираз не має змісту, оскільки на нуль ділити не можна.
Значення числового виразу дорівнює \(10\).
Вираз не має змісту.
Якщо вираз окрім чисел містить ще й букви (або тільки букви), які позначають числа або змінні, то його називають алгебраїчним виразом.
Алгебраїчні вирази
Областю визначення виразу або областю допустимих значень змінних (ОДЗ) у виразі називають всі можливі значення змінних, при яких цей вираз має зміст.
Можна обчислити числове значення алгебраїчного виразу при будь-якому значенні змінної з його області допустимих значень.
Приклад:
Знайди область визначення алгебраїчного виразу .
Розв'язання. Алгебраїчний дріб визначений при всіх значеннях змінної \(x\), при яких знаменник дробу \(x( x + 8 )\) не дорівнює \(0\). Тому, щоб знайти значення \(x\), які не належать області допустимих значень, необхідно знаменник \(x( x + 8 )\) прирівняти до нуля, тобто розв'язати рівняння:
\(x ( x + 8 ) = 0\).
Добуток дорівнює нулю тоді, коли хоча б один із множників дорівнює нулю. Отже, кожний множник прирівнюємо до нуля:
\(x = 0\) та \(x + 8 = 0\)
\(x = - 8\).
Відповідь. Область визначення алгебраїчного дробу — всі дійсні числа, крім \(0\) і \(-8\).
Алгебраїчні вирази поділяються на раціональні та ірраціональні, але зараз розглядатимемо лише раціональні вирази, а з ірраціональними виразами ознайомимося згодом.
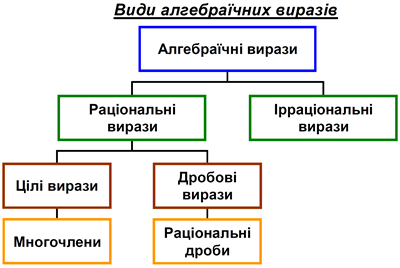
Алгебраїчний вираз, у якому є додавання, множення, ділення та піднесення до степеня (показник степеня — натуральне число), називають раціональним виразом.
Якщо раціональний вираз не містить дії ділення на змінну чи на вираз зі змінною, то його називають цілим.
Якщо раціональний вираз містить ділення на змінну чи на вираз зі змінною, то такий вираз називають дробовим.
Цілі вирази:
Дробові вирази:
Цілий раціональний вираз визначений при будь-яких значеннях змінних.
Дробовий раціональний вираз визначений при таких значеннях змінної, при яких знаменник дробу не дорівнює нулю.
1. Цілий вираз визначений при будь-яких значеннях змінної \(y\); область допустимих значень — всі дійсні числа.
2. Дробовий вираз не має змісту, якщо \(x = 8\) (якщо \(x = 8\), то знаменник \(x - 8 = 0\), а на нуль ділити не можна).
Отже, область визначення дробового виразу — всі дійсні числа, крім \(8\).
Дробовий раціональний вираз, чисельником і знаменником якого є многочлени, називають раціональним дробом.
Зверни увагу!
Областю допустимих значень раціонального дробу є всі значення змінної, при яких знаменник дробу НЕ дорівнює \(0\).
Будь-який дробовий раціональний вираз можна перетворити на раціональний дріб.