Як побудувати графік функції \(у = f(x + l)\), якщо відомий графік функції \(у = f(x)\)
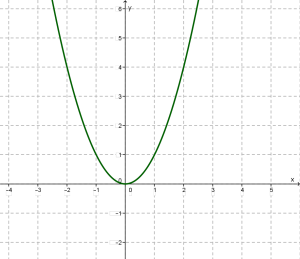
Для функції складемо таблицю значень:
| \(x\) | \(-3\) | \(-2\) | \(-4\) | \(-5\) | \(-1\) | \(-6\) | \(0\) |
| \(y\) | \(0\) | \(1\) | \(1\) | \(4\) | \(4\) | \(9\) | \(9\) |
Побудувавши точки \((-3; 0), (-2; 1), (-4; 1), (- 5; 4), (- 1; 4), (- 6; 9), (0; 9)\) на координатній площині і з'єднавши їх плавною кривою, отримаємо параболу:
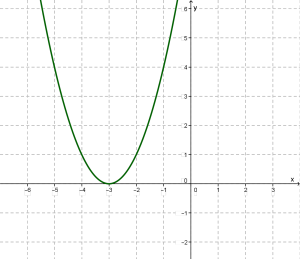
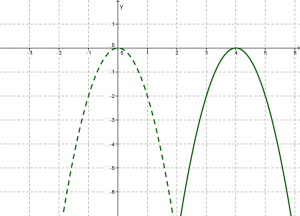
Тепер побудуємо в одній системі координат графіки функцій та .
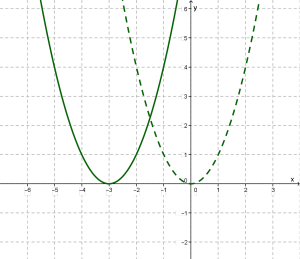
Зверни увагу!
Це точно така ж парабола, як і , але тільки зрушена уздовж осі \(x\) на \(3\) одиниці масштабу вліво. Вершина параболи тепер знаходиться в точці \((- 3; 0)\), а не в точці \((0; 0)\), як для параболи . Віссю симетрії служить пряма \(x = - 3\), а не \(x = 0\), як це було у випадку параболи .
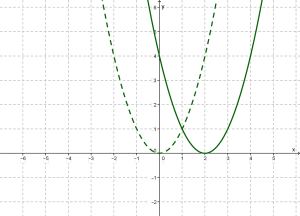
Точно так само йде справа і з графіками інших функцій.
Наприклад, графік функції — парабола, яка виходить з параболи зсувом (паралельним переносом) уздовж осі \(x\) на \(4\) одиниці масштабу вправо.
Наприклад, графік функції — парабола, яка виходить з параболи зсувом (паралельним переносом) уздовж осі \(x\) на \(4\) одиниці масштабу вправо.
Взагалі, справедливо наступне твердження:
щоб побудувати графік функції \(y = f(x + l)\), де \(l\) — задане додатне число, потрібно зрушити графік функції \(y = f(x)\) уздовж осі \(x\) на \(l\) одиниць масштабу вліво;
щоб побудувати графік функції \(y = f(x - l)\), де \(l\) — задане додатне число, потрібно зрушити графік функції \(y = f(x)\) уздовж осі \(x\) на \(l\) одиниць масштабу вправо.
щоб побудувати графік функції \(y = f(x - l)\), де \(l\) — задане додатне число, потрібно зрушити графік функції \(y = f(x)\) уздовж осі \(x\) на \(l\) одиниць масштабу вправо.
Зверни увагу!
Напрямок зсуву визначається знаком числа \(l\): при \(l > 0\) графік зсувається вліво, при \(l < 0\) - вправо.