Розв'язання задач за допомогою систем рівнянь

Система двох рівнянь з двома змінними може служити математичною моделлю реальної ситуації.

Розв'язання текстової задачі ділиться на три етапи:

Перший етап. Складання математичної моделі.
Другий етап. Робота зі складеною моделлю.
Третій етап. Відповідь на питання задачі.

Задача. Різниця катетів прямокутного трикутника дорівнює
\(23\) см, а його гіпотенуза дорівнює \(37\) см. Знайдіть площу трикутника.

Розв'язання.

Перший етап. Складання математичної моделі.

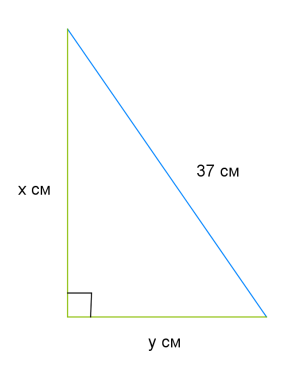
Позначимо довжину одного катета \(x\)см, а іншого \(y\)cм.

Тоді,

x - y = 23

— різниця катетів прямокутного трикутника.

Застосувавши теорему Піфагора, отримаємо друге рівняння:

\begin{array}{l} x^{2} + y^{2} = 37^{2} \\ x^{2} + y^{2} = 1369 \end{array}

Складаємо систему двох рівнянь з двома невідомими:

\{\begin{cases} x - y = 23 \\ x^{2} + y^{2} = 1369 \end{cases}

Другий етап. Робота зі складеною моделлю.

Виразимо \(x\) через \(y\) з першого рівняння системи.

\{\begin{cases} x = 23 + y \\ x^{2} + y^{2} = 1369 \end{cases}

Підставимо цей вираз замість \(x\) у друге рівняння системи.

\begin{array}{l} x^{2} + y^{2} = 1369 \\ {(23 + y)}^{2} + y^{2} = 1369 \\ 23^{2} + 46 y + y^{2} + y^{2} = 1369 \\ 2 y^{2} + 46 y + 529 - 1369 = 0 \\ 2 y^{2} + 46 y - 840 = 0 |: 2 \\ y^{2} - 23 y - 420 = 0 \\ y_{1} = \underline{12} \end{array}

y_{2} = - 35

(не підходить за умовою задачі)

Знайдемо \(x\) з першого рівняння системи.

x = 23 + 12 = \underline{35}

Третій етап. Відповідь на питання задачі.

Знайдемо площу прямокутного трикутника.

S = \frac{1}{2} xy = \frac{1}{2} \cdot 12 \cdot 35 = \frac{{}^{6}12 \cdot 35}{2_{1}} = 210 {см}^{2}

Відповідь:

S = 210 {см}^{2}

Знайшли помилку?

1. Розв'язання задач за допомогою систем рівнянь