Коренем \(n\)-ого степеня з дійсного числа a називається таке число, \(\ n\)-й степінь якого дорівнює \(a\) .
Арифметичним коренем \(n\)-ого степеня з невідємного числа \(a\) називається таке невідємне число, n-й степінь якого дорівнює a.
— корінь, n — показник кореня, a — підкореневий вираз.
Зверни увагу!
Корінь непарного степеня існує при будь-яких значеннях підкореневого виразу \(а\) (\(а\ є\ R\)).
Корінь парного степеня існує лише для невід'ємного підкореневого виразу \(а\) ( \(a ≥ 0\)).
Властивості коренів \(\ n\)-ого степеня:
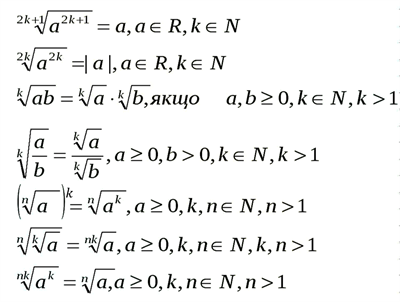
Детально повторити тему «Квадратні корені» можна в курсі «Алгебра» \(8\) клас, а теми «Поняття кореня n-го степеня з дійсного числа» та «Властивості кореня n-го степеня» — у курсі «Алгебра» \(10\) клас.