4. Степеневі функції (показник степеня — дробове від'ємне число)

 

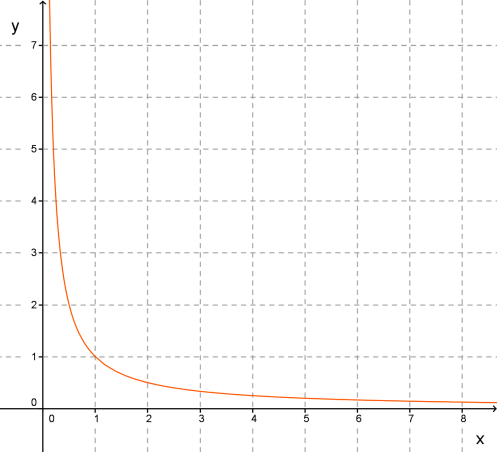
Графік має горизонтальну асимптоту \(y = 0\) і вертикальну асимптоту \(x =0.\)

\(1)\) $D(f)=\left(0\right.;\left.+\mathrm{\infty }\right)$\(;\)

\(2)\) $E(f)=\left(0\right.;\left.+\mathrm{\infty }\right)$\(;\)

\(3)\) не є ні парною, ні непарною;

\(4)\) спадає при $x\in \left(0\right.;\left.+\mathrm{\infty }\right)$\(;\)

\(5)\) не має ні найбільшого, ні найменшого значення;

\(6)\) необмежена зверху, обмежена знизу;

\(7)\) опукла вниз;

\(8)\) неперервна.

 

Уточненя: правло подано для нецілого $a=-\frac{m}{n}$ , де \(x>0\) (аби уникнути неоднозначностей). Якщо показник має непарний знаменник \(n\), то функція фактично визначена для всіх \(x\), де $x^m$ має зміст. Це можна побачити на графіках, побудованих сучасними графічними інструментами. Більш детально про властивості таких функцій, ви зможете дізнатись при глибшому подальшому вивченні функцій.