Розглянемо графіки степеневих функцій з додатним дробовим показником \(.\)
\(1.\) Степенева функція \(,\) де — неправильний дріб (чисельник більший від знаменника).
Графік — вітка параболи.
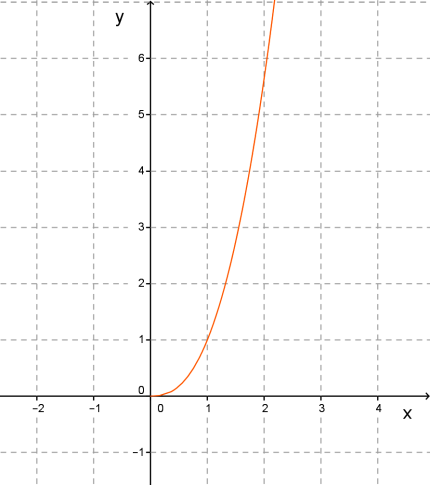
Властивості функції \(,\) де
\(1)\) \(;\)
\(2)\) \(;\)
\(3)\) не є ні парною, ні непарною;
\(4)\) зростає при \(;\)
\(5)\) не має найбільшого значення, \(;\)
\(6)\) необмежена зверху, обмежена знизу;
\(7)\) опукла вниз;
\(8)\) неперервна.
\(2.\) Степенева функція \(,\) де — правильний дріб (чисельник менший від знаменника).
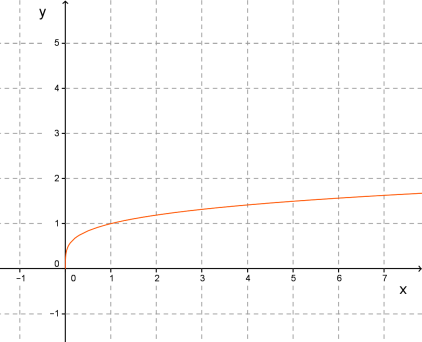
Властивості функції \(,\) де
\(1)\) \(;\)
\(2)\) \(;\)
\(3)\) не є ні парною, ні непарною;
\(4)\) зростає при \(;\)
\(5)\) не має найбільшого значення, \(;\)
\(6)\) необмежена зверху, обмежена знизу;
\(7)\) опукла вгору;
\(8)\) неперервна.
Цікаво: якщо Ви плануєте більш глибоко вивчати математику (за межами шкільної програми), зверніть увагу на випадок, коли знаменник \(n\), є непарним числом (наприклад ).
Область визначення такої функції, включатиме від'ємні числа (бо корінь непарного степеня існує й для від'ємного числа).
Якщо \(m\) парне (наприклад ), функція буде парною.
Якщо \(m\) непарне (наприклад ), функція буде непарною.
Аби наочно побачити, як виглядатимуть дані відмінності, можете скористатись сучасними графічними інструментами.