Тангенс і котангенс гострого кута прямокутного трикутника визначається так:
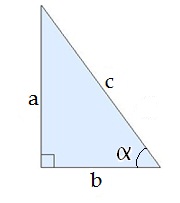 |
Щоб зчитати значення тангенса кута повороту, через точку \((1;0)\) проводиться дотична до одиничного кола. Ця пряма називається віссю тангенса. Значення тангенса читаються з осі \(Oy\). | 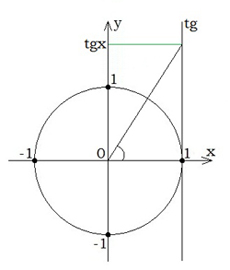 |
Щоб зчитати значення котангенса кута повороту, через точку \((0;1)\) проводиться дотична до одиничного кола. Ця пряма називається віссю котангенса. Значення котангенса читаються з осі \(Ox\). | 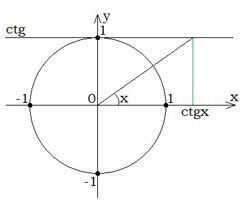 |
Найчастіше одиничне коло використовується для визначення знака тригонометричної функції, числові значення знаходяться в таблицях або обчислюються за допомогою калькулятора.
Знаки тангенса і котангенса у чвертях визначаються, використовуючи вже відомі знаки синуса і косинуса і основні тригонометричні тотожності:
Щоб визначити знак: 1. на одиничному колі позначається кут повороту; 2. визначається знак синуса; 3. визначається знак косинуса; 4. визначається знак частки. На малюнку приклад, як визначити знак тангенса кута в \(III\) чверті. | 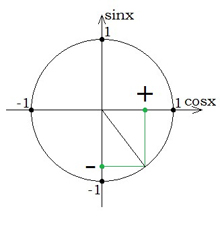 |
| Знаки тангенса і котангенса у чвертях не відрізняються. На малюнку дані знаки тангенса і котангенса у чвертях. | 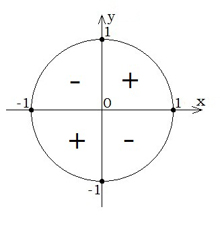 |
Важливо вміти зчитувати з одиничного кола наступні значення тангенса і котангенса:
\(tg\) \(0^{\circ}=0\) \(tg\) \(90^{\circ}\) не існує \(tg\) \(180 ^{\circ}=0\) \(tg\) \(270^{\circ}\) не існує \(tg\) \(360^{\circ}=0\) | \(ctg\) \(0 ^{\circ}\) не існує \(ctg\) \(90^{\circ}=0\) \(ctg\) \(180^{\circ}\) не існує \(ctg\) \(270^{\circ}=0\) \(ctg\) \(360 ^{\circ}\) не існує |
Значення тригонометричних функцій, які треба знати напам'ять.
| \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | |
| \(sin\) | |||
| \(cos\) | |||
| \(tg\) | \(1\) |
| \(ctg\) | \(1\) |