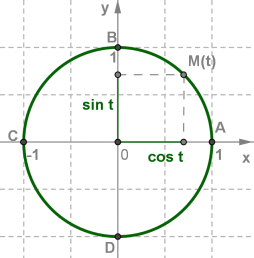
Якщо точка \(M\) числового кола відповідає числу \(t\), тоді абсцису точки \(M\) називають косинусом числа \(t\) та позначають \(cos\) \(t\),а ординату точки \(M\) називають синусом числа \(t\) та позначають \(sin\) \(t\).
Отже, якщо
тоді
Звідси, (див. рис.)
Відношення синуса числа \(t\) до косинуса того ж числа називають тангенсом числа \(t\) і позначають \(tg\) \(t\).
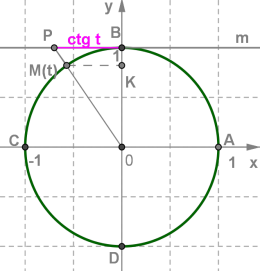
Відношення косинуса числа \(t\) до синуса того ж числа називають котангенсом числа \(t\) і позначають \(ctg\) \(t\).
З рівняння числового кола , замінюючи \(x\) і \(y\) на \(cos\) \(t\) і \(sin\) \(t\), отримуємо рівність
Відзначимо кілька важливих властивостей синуса, косинуса, тангенса і котангенса.
Властивість 1. Для будь-якого значення \(t\) справедливі рівності:
Властивість 2. Для будь-якого значення \(t \) справедливі рівності:
Властивість 3. Для будь-якого значення \(t\) справедливі рівності:
Будуть правильні й такі рівності:
Властивість 4. Для будь-якого значення \(t\) справедливі рівності:
Для синуса і косинуса є геометрична ілюстрація на числовому колі.
Дано геометричну ілюстрацію для тангенса і котангенса.
Проведемо спочатку в координатній площині до числового кола дотичну в точці \(A\).
Цю дотичну \(l\) будемо вважати числовою прямою, орієнтованою також, як вісь \(y\) і з початком в точці \(A\) (див. рис.)
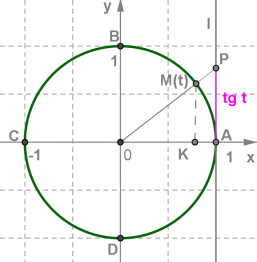 |
З подібності трикутників \(OMK\) і \(OPA\), отримаємо рівність:
Тобто \(PA = tg\) \(t\).
|
Отже, якщо числу \(t\) відповідає на числовому колі точка \(M\), тоді, провівши пряму \(OM\), отримаємо в перетині її з числовою прямою \(l\) точку \(P\), яка має на числовій прямій \(l\) координату \(tg\) \(t\).
Числову пряму \(l\) називають лінією тангенсів.
Аналогічно можна отримати лінію котангенсів — числова пряма \(m\) з початком в точці \(B\) (див. рис.).