1. Властивості функції y = sinx та її графік

Графік цієї функції можна побудувати таким же способом, як і графік функції $y=\mathit{cosx}$, починаючи з побудови, наприклад, на відрізку $\left[0;\mathrm{\pi }\right]$. 

Однак простіше застосувати формулу $\mathit{sinx}=\mathit{cos}\left(x-\frac{\mathrm{\pi }}{2}\right)$, яка показує, що графік функції $y=\mathit{sinx}$ можна отримати зсувом графіка функції  $y=\mathit{cosx}$ уздовж осі абсцис праворуч на $\frac{\mathrm{\pi }}{2}$. 

 

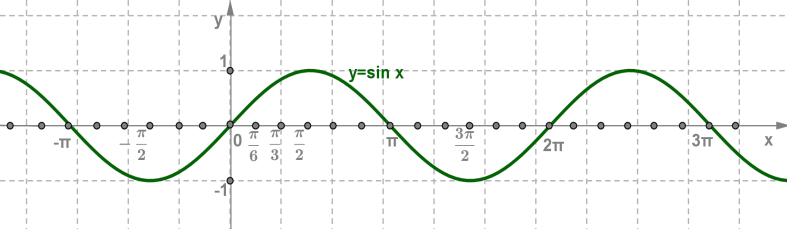
Графік функції $y=\mathit{sinx}$.

1. Область визначення - множина $\mathrm{ℝ}$ всіх дійсних чисел.

2. Множина значень - відрізок $\left[-1;1\right]$.

3. Функція $y=\mathit{sinx}$ періодична з періодом \(T =\) $2\mathrm{\pi }$. 

4. Функція $y=\mathit{sinx}$ - непарна.

5. Функція $y=\mathit{sinx}$ приймає:
- значення, яке дорівнює \(0\), при  $x=\mathrm{\pi }n,n\in \mathrm{\mathbb{Z}}$; 
- найбільше значення, яке дорівнює \(1\), при $x=\frac{\mathrm{\pi }}{2}+2\mathrm{\pi }n,n\in \mathrm{\mathbb{Z}}$; 
- найменше значення, яке дорівнює \(-1\), при $x=-\frac{\mathrm{\pi }}{2}+2\mathrm{\pi }n,n\in \mathrm{\mathbb{Z}}$; 
- додатні значення на інтервалі $\left(0;\mathrm{\pi }\right)$ і на інтервалах, одержаних зсувами цього інтервалу на $2\mathrm{\pi }n,n\in \mathrm{\mathbb{Z}}$;

- від'ємні значення на інтервалі $\left(\mathrm{\pi };2\mathrm{\pi }\right)$ і на інтервалах, одержаних зсувами цього інтервалу на $2\mathrm{\pi }n,n\in \mathrm{\mathbb{Z}}$;

6. Функція $y=\mathit{sinx}$

- зростає на відрізку

 $\left[-\frac{\mathrm{\pi }}{2};\frac{\mathrm{\pi }}{2}\right]$  і на інтервалах, одержаних зсувами цього інтервалу на $2\mathrm{\pi }n,n\in \mathrm{\mathbb{Z}}$;
- спадає на відрізку

 $\left[\frac{\mathrm{\pi }}{2};\frac{3\mathrm{\pi }}{2}\right]$  і на інтервалах, одержаних зсувами цього інтервалу на $2\mathrm{\pi }n,n\in \mathrm{\mathbb{Z}}$.