Метод, заснований на використанні графічних ілюстрацій або будь-яких властивостей функцій.
В одній системі координат будуємо графіки функцій, записані в лівій і в правій частинах рівняння, потім, знаходимо точку (точки) їх перетину. Абсциса знайденої точки є розв'язком рівняння.
Приклад:
\(1.\) Розв'язати рівняння
Побудуємо в одній системі координат графіки функцій і
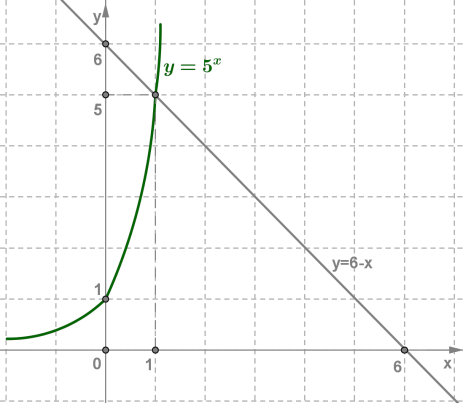
Вони перетинаються в одній точці (1; 5). Перевірка показує, що насправді точка (1; 5) задовольняє і рівняння , і рівняння .
Абсциса цієї точки служить єдиним коренем заданого рівняння,
оскільки — зростаюча функція, а — спадна.
Отже, рівняння має єдиний корінь .
Приклад:
\(2.\) Розв'язати рівняння: ;
Побудувавши в одній системі координат графіки функцій і ,
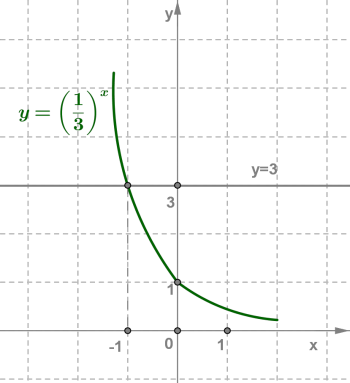
помічаємо (див. рис.), що графіки мають одну спільну точку (-1; 3). Отже, рівняння має єдиний корінь .
Отже, рівняння має корінь .