Першими числами, якими почали користуватися люди — це натуральні числа. Ці числа нам відомі з дитинства, коли ми вчилися рахувати предмети.
Натуральними числами називають числа, що використовуються під час лічби.
Усі натуральні числа утворюють множину натуральних чисел, яку позначають буквою \(\mathbb{N}\).
У подальшому, практичні потреби людей спричинили виникнення дробових чисел.
Згодом з’являється необхідність розглядати величини, для характеристики яких додатних чисел виявилось замало. Так виникли від’ємні числа.
Цілі числа — це натуральні числа, протилежні їм числа та число 0.
Усі цілі числа утворюють множину цілих чисел, яку позначають буквою \(\mathbb{Z}\).
\(-5\in\mathbb{Z},\) \(-5\notin\mathbb{N};\) \(0\in\mathbb{Z},\) \(0\notin\mathbb{N};\) \(7\in\mathbb{Z},\) \(7\in\mathbb{N}.\)
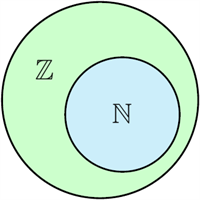
Отже, множина натуральних чисел є підмножиною множини цілих чисел, тобто \(\mathbb{N}\subset\mathbb{Z}.\)
Зверни увагу!
Будь-яке натуральне число є й цілим.
Однак, не будь-яке ціле число є натуральним!
Схема, що зображена на рисунку, показує, як співвідносяться множини \(\mathbb{N}\) і \(\mathbb{Z}.\)