Раціональні числа — це цілі та дробові, як додатні, так і від’ємні числа.
Усі раціональні числа утворюють множину раціональних чисел, яку позначають буквою \(\mathbb{Q}\).
Приклад:
\(\dfrac{3}{5}\in\mathbb{Q};\) \(\dfrac{3}{5}\notin\mathbb{N};\) \(\dfrac{3}{5}\notin\mathbb{Z};\)
\(-0,3\in\mathbb{Q};\) \(-0,3\notin\mathbb{N};\) \(-0,3\notin\mathbb{Z};\)
\(-5\in\mathbb{Q};\) \(-5\notin\mathbb{N};\) \(-5\in\mathbb{Z};\)
\(9\in\mathbb{Q};\) \(9\in\mathbb{N};\) \(9\in\mathbb{Z}.\)
Зрозуміло, що множина цілих чисел є підмножиною множини раціональних чисел, тобто \(\mathbb{Z}\subset\mathbb{Q}.\)
Отже, \(\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}.\)
Зверни увагу!
Будь-яке ціле число є й раціональним.
Однак, не будь-яке раціональне число є цілим!
Будь-яке натуральне число є й раціональним.
Однак, не будь-яке раціональне число є натуральним!
Схема, що зображена на рисунку, показує, як співвідносяться множини \(\mathbb{N},\) \(\mathbb{Z}\) і \(\mathbb{Q}.\)
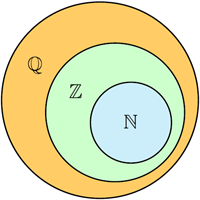
Множини \(\mathbb{N},\) \(\mathbb{Z}\) і \(\mathbb{Q}\) є нескінченими множинами.
Будь-яке раціональне число можна подати у вигляді \(\dfrac{m}{n},\) де \(m\) — ціле число, \(n\) — натуральне число.
Приклад:
\(7=\dfrac{7}{1};\) \(-9=\dfrac{-9}{1};\) \(5\dfrac{2}{3}=\dfrac{17}{3};\) \(0,6=\dfrac{3}{5};\) \(0=\dfrac{0}{8};\) \(3,7=\dfrac{37}{10}.\)
З можливістю такого подання й пов’язана назва «раціональне число», оскільки одним із значень латинського слова ratio є «відношення».
Будь-яке раціональне число можна також подати у вигляді десяткового дробу. Для цього достатньо чисельник дробу поділити на його знаменник.
Приклад:
\(\dfrac{3}{8}=0,375;\) \(\dfrac{-9}{4}=-2,25;\) \(\dfrac{7}{11}=0,636363...=0,(63).\)
В останньому випадку ми отримали нескінченний десятковий дріб. У записі \(0,636363...\) цифри \(6\) і \(3\) періодично повторюються.
Групу цифр, яка повторюється, називають періодом дробу й записують у круглих дужках.
Дроби \(\dfrac{3}{8}\) і\(\dfrac{-9}{4}\) також можна подати у вигляді нескінченних десяткових періодичних дробів, дописавши праворуч як десяткові знаки нескінченну кількість нулів:
\(\dfrac{3}{8}=0,375=0,375000...=0,375(0);\)
\(\dfrac{-9}{4}=-2,25=-2,25000...=-2,25(0).\)
Отже,
кожне раціональне число можна подати у вигляді нескінченного десяткового періодичного дробу.
Справджується й обернене твердження:
кожний нескінченний десятковий періодичний дріб є записом деякого раціонального числа.
Приклад:
\(1,5000...=1,5=\dfrac{15}{10}=\dfrac{3}{2};\) \(0,(6)=\dfrac{2}{3};\) \(-1,(45)=-1\dfrac{5}{11}.\)
У правильності цих рівностей легко переконатися, виконавши відповідне ділення.
А чи можна записати будь-який нескінченний десятковий періодичний дріб у вигляді звичайого дробу? Відповідь ствердна — так! Але ми навчимося це робити у 9 класі.
Зверни увагу!
Сума й добуток двох натуральних чисел є натуральними числами.
Проте різниця натуральних чисел не завжди має таку властивість. Наприклад, \((3-5)\notin\mathbb{N}.\)
Сума, різниця й добуток двох цілих чисел є цілими числами.
Проте частка цілих чисел не завжди має таку властивість. Наприклад, \(\dfrac{3}{5}\notin\mathbb{Z}.\)
Сума, різниця, добуток і частка (крім ділення на нуль) двох раціональних чисел є раціональними числами.
Отже,
дії віднімання та ділення натуральних чисел можуть вивести результат за межі множини \(\mathbb{N}\);
дія ділення для цілих чисел — за межі множини \(\mathbb{Z}\);
проте виконання будь-якої із чотирьох арифметичних дій з раціональними числами не виводить результат за межі множини \(\mathbb{Q}\).
дія ділення для цілих чисел — за межі множини \(\mathbb{Z}\);
проте виконання будь-якої із чотирьох арифметичних дій з раціональними числами не виводить результат за межі множини \(\mathbb{Q}\).
