Дійсні числа — це всі числа, які можна зобразити на координатній прямій. Це — раціональні та ірраціональні числа.
Усі дісні числа утворюють множину дійсних чисел, яку позначають буквою \(\mathbb{R}\) (першою буквою латинського слова realis — «реальний», «той, що існує насправді».
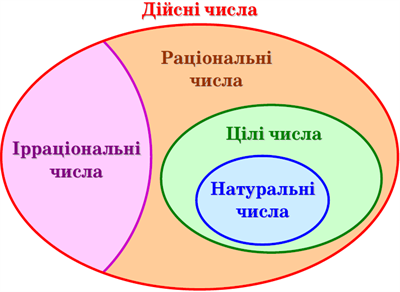
Отже, \(\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}\subset\mathbb{R}.\)
Схема, що зображена на рисунку, показує, як співвідносяться множини \(\mathbb{N},\) \(\mathbb{Z},\) \(\mathbb{Q}\) і \(\mathbb{R}.\)
Зверни увагу!
Над дійсними числами можна виконувати чотири арифметичні дії (крім ділення на нуль), у результаті отримуватимемо дійсне число.
Цим діям притаманні звичні для нас властивості:
| \(a+b=b+a\) | Переставна властивість додавання |
| \(ab=ba\) | Переставна властивість множення |
| \((a+b)+c=a+(b+c)=b+(a+c)\) | Сполучна властивість додавання |
| \((ab)c=a(bc)=b(ac)\) | Сполучна властивість множення |
| \(a(b+c)=ab+ac\) | Розподільна властивість множення відносно додавання |
| \(a(b-c)=ab-ac\) |
Розподільна властивість множення відносно віднімання
|
Ірраціональні числа, які записано у вигляді нескінченних неперіодичних десяткових дробів, порівнюють між собою за тими самими правилами, що й скінченні десяткові дроби.
Приклад:
Порівняй \(\sqrt{2}\) і \(1,4\).
Розв’язання
Подамо \(\sqrt{2}\) у вигляді десяткового дробу з точністю до сотих: \(\sqrt{2}\approx1,41.\)
Тоді \(1,41>1,4\), а отже й \(\sqrt{2}>1,4.\)
Відповідь: \(\sqrt{2}>1,4.\)
Приклад:
Порівняй \(-\sqrt{7}\) і \(-2,64\).
Розв’язання
Подамо \(-\sqrt{7}\) у вигляді десяткового дробу з точністю до тисячних: \(-\sqrt{2}\approx-2,645.\)
Тоді \(-2,645<-2,64\), а отже й \(-\sqrt{7}<-2,64.\)
Відповідь: \(-\sqrt{7}<-2,64.\)