Ми ознайомилися з новою дією — добуванням квадратного кореня.
Чи завжди квадратний корінь з невід’ємного раціонального числа є раціональним числом? Чи не виведе результат за межі множини \(\mathbb{Q}\)?
Розглянемо рівняння \(x^2=2\). Оскільки \(2>0\), то це рівняння має два корені: \(\sqrt{2}\) і \(-\sqrt{2}\) (див. рисунок).
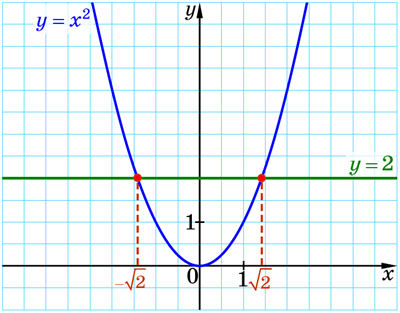
Однак не існує раціонального числа, квадрат якого дорівнює 2, тобто числа \(\sqrt{2}\) і \(-\sqrt{2}\) не є раціональними (див. доведення цього факту нижче).
Ці числа є прикладами ірраціональних чисел (префікс «ір» означає «заперечення», тобто ірраціональні — означає не раціональні).
Отже, дія добування квадратного кореня з раціонального числа може вивести результат за межі множини \(\mathbb{Q}\).
Ірраціональними числами називають числа, які не можна записати у вигляді \(\dfrac{m}{n}\), де \(m\) — ціле число, а \(n\) — натуральне.
Ірраціональні числа можуть бути подані у вигляді нескінченних неперіодичних десяткових дробів.
Наприклад, ірраціональними є числа \(\pi\), \(\sqrt{2}\), \(-\sqrt{7}\) тощо. Наближені значення таких чисел можна знаходити з певною точністю (тобто округленими до певного розряду) за допомогою калькулятора або комп’ютера:
\(\pi\approx3,1415926;\) \(\sqrt{2}\approx1,4142135;\) \(-\sqrt{7}\approx-2,6457513.\)
Приклад:
Доведи, що число \(\sqrt{2}\) — ірраціональне.
Доведення
Припустимо, що число \(\sqrt{2}\) раціональне. Тоді його можна подати у вигляді нескоротного дробу \(\dfrac{m}{n}\), де \(m\) і \(n\) — натуральні числа.
Маємо: \(\sqrt{2}=\dfrac{m}{n}.\)
Тоді \(\left(\sqrt{2}\right)^2=\left(\dfrac{m}{n}\right)^2;\) \(2=\dfrac{m^2}{n^2};\) \(m^2=2n^2.\)
З останньої рівності випливає, що число \(m^2\) парне. А це означає, що парним є і число \(m\).
Тоді нехай \(m=2k\), де \(k\) — деяке натуральне число.
Маємо: \(\left(2k\right)^2=2n^2;\) \(4k^2=2n^2;\) \(n^2=2k^2.\)
Звідси випливає, що число \(n^2\), а отже, і число \(n\) парні.
Таким чином, чисельник і знаменник дробу \(\dfrac{m}{n}\) — парні числа.
Тоді цей дріб є скоротним. Отримали суперечність.
Отже, число \(\sqrt{2}\) не можна подати у вигляді нескоротного дробу \(\dfrac{m}{n}\), де \(m\) і \(n\) — натуральні числа, тобто число \(\sqrt{2}\) — ірраціональне, що й треба було довести.
