1. Квадратична функція

У 7-му класі ми вивчали функції \(у = m\), \(у = kx\), \(у = kx + m\), $y=x^2$ та дійшли висновку, що рівняння з двома змінними вигляду \(у = f(x)\) (функція) є математичною моделлю, зручною для того, аби, надавши конкретного значення незалежній змінній \(x\) (аргументу), обчислити відповідне значення залежної змінної \(y\).

 

Насправді функція $y=k{x}^2$ в одному випадку нам трохи знайома.

 

Дивися: якщо \(k = 1\), то ми отримуємо $y=x^2$. Цю функцію ми вивчили в 7-му класі. Ти, напевно, пам'ятаєш, що її графіком є парабола.

 

 

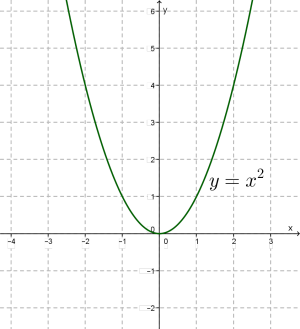
Обговоримо, що відбувається за інших значень коефіцієнта \(k\).

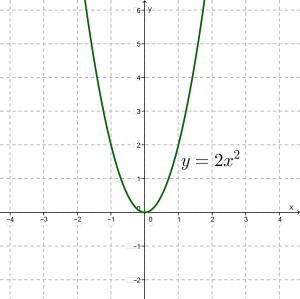
Розглянемо дві функції: $y=2x^2$ та $y=0.5x^2$. Складемо таблицю значень для першої функції$y=2x^2$.

 

 

Побудуємо точки \((0; 0), (1; 2), (-1; 2), (2; 8), (-2; 8), (1,5; 4,5), (-1,5; 4,5)\) на координатній площині; вони намічають деяку лінію, проведемо її.

 

 

Складемо таблицю значень для другої функції $y=0.5x^2$.

 

 

Побудуємо точки \((0; 0), (1; 0,5), (-1; 0,5), (2; 2), (-2; 2), (3; 4,5), (-3; 4,5)\) на координатній площині; вони намічають деяку лінію, проведемо її.

 

 

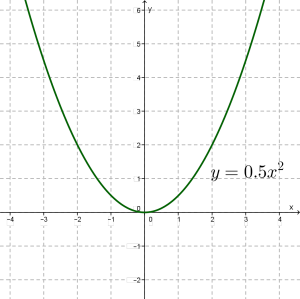
Порівняй отримані малюнки. Проведені лінії схожі, чи не так? Кожну з них називають параболою.

Точно так само відбувається з будь-якою іншою функцією вигляду $y=k{x}^2$, де \(k > 0\).

 

Графіком її є парабола з вершиною в початку координат, вітки параболи спрямовані вгору, причому тим крутіше, чим більше коефіцієнт \(k\).

 

Вісь \(y\) є віссю симетрії параболи.

 

До речі, заради лаконічності висловлювання математики часто замість довгої фрази «парабола, що слугує графіком функції $y=k{x}^2$», говорять так: «парабола $y=k{x}^2$», а замість терміна «вісь симетрії параболи» використовують термін «вісь параболи».

 

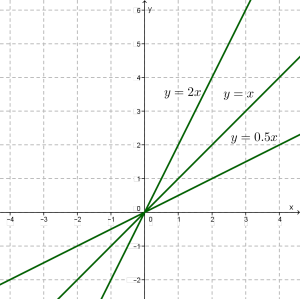
Ти помічаєш, що є аналогія з функцією \(у = kx\)?

 

Якщо \(k > 0\), то графіком функції \(у = kx\) є пряма, що проходить через початок координат (пам'ятаєш, ми говорили коротко: пряма \(у = kx\)), причому і тут від величини коефіцієнта \(k\) залежить «ступінь крутизни» прямої.

 

Це добре видно на малюнку, де в одній системі координат зображені графіки лінійних функцій \(у = kx\) за трьох значень коефіцієнта \(k\).

 

 

Повернемося до функції $y=k{x}^2$. Розглянемо випадки від'ємного коефіцієнта \(k\).

 

Побудуємо, наприклад, графік функції $y=-x^2$ (тут \(k = -1\)). Складемо таблицю значень.

 

 

Побудуємо точки \((0; 0), (1; -1), (-1; -1), (2; -4), (-2; -4), (3; -9), (- 3; - 9)\) на координатній площині; вони намічають деяку лінію, проведемо її.

 

 

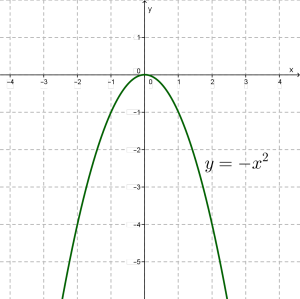
Це парабола з вершиною в точці \((0; 0)\), вісь \(y\) — вісь симетрії, але на відміну від випадку, коли \(k> 0\), на цей раз гілки параболи спрямовані вниз. Аналогічно відбувається і з іншими від'ємними значеннями коефіцієнта \(k\).

 

Зазначимо, що парабола $y=k{x}^2$ дотикається до осі \(x\) в точці \((0; 0)\), тобто одна вітка параболи плавно переходить в іншу, ніби притискаючись до осі \(x\).

 

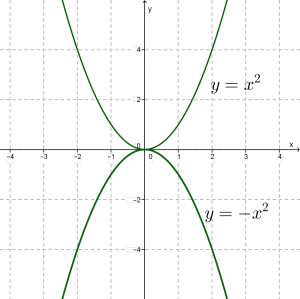
Якщо побудувати в одній системі координат графіки функцій $y=k{x}^2$ та $y=-x^2$, то нескладно помітити, що ці параболи симетричні одна одній щодо осі \(x\). Це добре видно на малюнку.

 

 

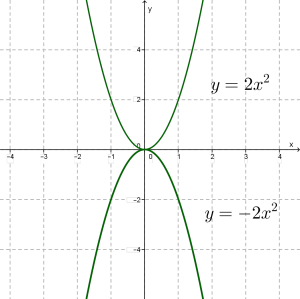
Так само симетричні одна одній щодо осі \(x\) параболи $y=2x^2$ та  $y=-2x^2$.