Дію знаходження арифметичного квадратного кореня називають добуванням квадратного кореня.
З невеликих чисел квадратний корінь бажано добувати усно.
Часто використовувані квадрати натуральних чисел:
| \(x\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) | \(9\) | \(10\) |
| \(x^2\) | \(1\) | \(4\) | \(9\) | \(16\) | \(25\) | \(36\) | \(49\) | \(64\) | \(81\) | \(100\) |
| \(x\) | \(11\) | \(12\) | \(13\) | \(14\) | \(15\) | \(16\) | \(17\) | \(18\) | \(19\) | \(20\) |
| \(x^2\) | \(121\) | \(144\) | \(169\) | \(196\) | \(225\) | \(256\) | \(289\) | \(324\) | \(361\) | \(400\) |
Добувати квадратний корінь з більших чисел допоможе таблиця квадратів двоцифрових натуральних чисел або калькулятор.
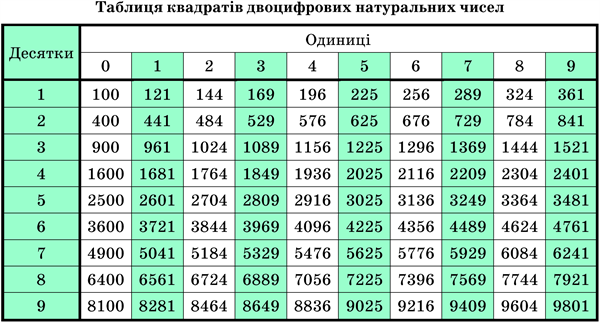
Приклад:
Знайди значення кореня \(\sqrt{3969}.\)
Розв’язання
За таблицею квадратів двоцифрових натуральних чисел маємо \(63^2=3969,\) тому \(\sqrt{3969}=63.\)
Відповідь: \(63\).
Приклад:
Обчисли \(\sqrt{29^2-21^2}.\)
Розв’язання
Спочатку знайдемо значення підкореневого виразу \(29^2-21^2\), а потім добудемо з нього корінь:
\(\sqrt{29^2-21^2}=\sqrt{841-441}=\sqrt{400}=20.\)
Відповідь: \(20\).