Розглянемо рівняння \(\sqrt{x}=m,\) де \(m\) — деяке число.
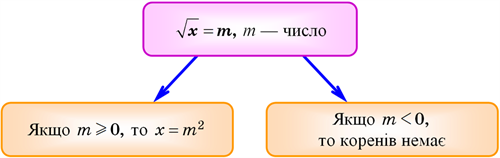
Якщо \(m\ge{0},\) то з означення квадратного кореня слідує, що \(x=m^2.\)
Якщо \(m<0,\) то рівняння не має коренів, оскільки за означенням квадратного кореня число \(\sqrt{x}\) — невід’ємне.
Отже, маємо алгоритм розв’язування рівняння \(\sqrt{x}=m\). Подамо його у вигляді схеми:
Приклад:
Розв’яжи рівняння \(\sqrt{x}=8.\)
Розв’язання
\(\sqrt{x}=8;\)
\(x=8^2;\)
\(x=64.\)
Відповідь: \(64.\)
Приклад:
Розв’яжи рівняння \(\sqrt{x}=-5.\)
Розв’язання
\(\sqrt{x}=-5<0.\)
Відповідь: рівняння коренів не має.
Розв’язання
\(\sqrt{x}=-5<0.\)
Відповідь: рівняння коренів не має.
Приклад:
Розв’яжи рівняння \(\sqrt{3x+4}=7.\)
Розв’язання
\(\sqrt{3x+4}=7;\)
\(3x+4=7^2;\)
\(3x+4=49;\)
\(3x=49-4;\)
\(3x=45;\)
\(x=45:3;\)
\(x=15.\)
Відповідь: \(15.\)
Приклад:
Розв’яжи рівняння \(\dfrac{1}{2}\sqrt{x}-3=0.\)
Розв’язання
\(\dfrac{1}{2}\sqrt{x}-3=0;\)
Розв’язання
\(\dfrac{1}{2}\sqrt{x}-3=0;\)
\(\dfrac{1}{2}\sqrt{x}=3;\)
\(\sqrt{x}=3·2;\)
\(\sqrt{x}=6;\)
\(x=6^2;\)
\(x=36.\)
Відповідь: \(36.\)
Приклад:
Розв’яжи рівняння \(\sqrt{1+\sqrt{x+2}}=2.\)
Розв’язання
\(\sqrt{1+\sqrt{x+2}}=2;\)
Розв’язання
\(\sqrt{1+\sqrt{x+2}}=2;\)
\(1+\sqrt{x+2}=2^2;\)
\(1+\sqrt{x+2}=4;\)
\(\sqrt{x+2}=4-1;\)
\(\sqrt{x+2}=3;\)
\(x+2=3^2;\)
\(x+2=9;\)
\(x=9-2;\)
\(x=7.\)
Відповідь: \(7.\)
