Розглянемо множину цифр: \(A=\{0,1,2,3,4,5,6,7,8,9\}.\)
Виокремимо з множини \(A\) її елементи, які є парними цифрами. Отримаємо множину \(B=\{0,2,4,6,8\}\), усі елементи якої є елементами множини \(A\).
Множину \(B\) називають підмножиною множини \(A\), якщо кожний елемент множини \(B\) є елементом множини \(A\).
Це записують так: \(B\subset{A}\) або \(A\supset{B}\) (читають: «множина \(B\) є підмножиною множини \(A\)» або «множина \(A\) містить множину \(B\)»).
Розглянемо приклади:
- множина учнів вашого класу є підмножиною множини учнів вашої школи;
- множина ссавців є підмножиною множини хребетних;
- множина точок променя \(CB\) є підмножиною множини точок прямої \(AB\) (див. рисунок);
- множина прямокутників є підмножиною множини паралелограмів;
- \(\{a\}\subset\{a,b\}\).
Для ілюстрації співвідношень між множинами користуються схемами, які називають діаграмами Ейлера.
На рисунку зображено множину \(A\) (більший круг) і множину \(B\) (менший круг, який міститься в більшому).
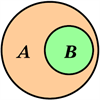
Ця схема означає, що \(B\subset{A}\) або \(A\supset{B}\).
З означень підмножини та рівності множин випливає, що коли \(A\subset{B}\) і \(B\subset{A}\), то \(A=B\).
Якщо в множині \(B\) немає елемента, який не належить множині \(A\), то множина \(B\) є підмножиною множини \(A\).
З огляду на ці міркування порожню множину вважають підмножиною будь-якої множини. Справді, порожня множина не містить жодного елемента, отже, у ній немає елемента, який не належить заданій множині. Тому для будь-якої множини \(A\) справедливо твердження: \(\varnothing \subset{A}\).
Будь-яка множина \(A\) є підмножиною самої себе, тобто \(A\subset{A}\).
Приклад:
Випишіть усі підмножини множини \(A=\{a,b,c\}.\)
Розв’язання
Маємо: \(\{a\}\), \(\{b\}\), \(\{c\}\), \(\{a,b\}\), \(\{b,c\}\), \(\{a,c\}\), \(\{a,b,c\}\), \(\varnothing\).
