Розглянемо рівняння \(x^2 = a\), де \(a\) — деяке число.
Оскільки квадрат числа не може дорівнювати від’ємному числу, то, коли \(a < 0\), рівняння \(x^2 = a\) не має розв’язків, що можна записати так: \(х \in \varnothing.\)
Якщо \(a = 0\), то єдиним коренем рівняння \(x^2 = 0\) є число \(0\).
Якщо \(a > 0\), то коренями рівняння \(x^2=a\) є числа \(\sqrt{a}\) і \(-\sqrt{a}\).
Справді, \(\left(\sqrt{a}\right)^2=a\) і \(\left(-\sqrt{a}\right)^2=a\).
Аби впевнитися, що рівняння \(x^2=a\), де \(a > 0\), інших коренів не має, звернімося до графічної інтерпретації його розв’язування.
Побудуємо в одній системі координат графіки функцій \(f(x)=x^2\) та \(g(x)=a\), де \(a>0\) (див. рисунок).
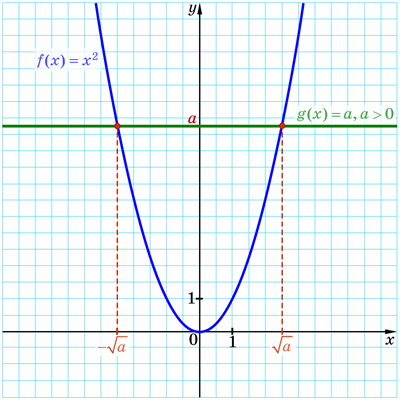
Графіки перетнулися лише двічі: у точках з абсцисами \(\sqrt{a}\) і \(-\sqrt{a}\).
Систематизуємо алгоритм розв’язування рівняння \(x^2=a\) у вигляді схеми:
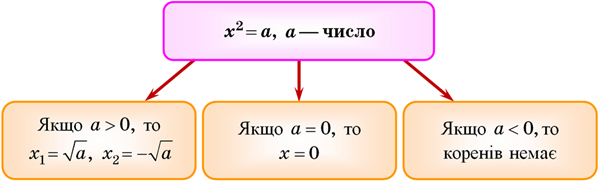
Приклад:
Розв’яжи рівняння \(x^2=9.\)
Розв’язання
\(x_1=\sqrt{9}=3,\) \(x_2=-\sqrt{9}=-3.\)
Відповідь: \(\pm{3}.\)
Приклад:
Розв’яжи рівняння \(x^2=-5.\)
Розв’язання
\(x^2=-5<0.\)
Отже, рівняння коренів не має.
Відповідь: \(\varnothing.\)
Приклад:
Розв’яжи рівняння \(x^2=5.\)
Розв’язання
\(x_1=\sqrt{5},\) \(x_2=-\sqrt{5}.\)
Ці корені є ірраціональними числами.
Відповідь: \(\pm{\sqrt{5}}.\)
Приклад:
Розв’яжи рівняння \(\left(2x+1\right)^2=5.\)
Розв’язання
| Маємо: |
\(2x+1=\sqrt{25}\)
\(2x+1=5;\)
\(2x=5-1;\)
\(2x=4;\)
\(x=4:2;\)
\(x=2;\)
|
або |
\(2x+1=-\sqrt{25};\)
\(2x+1=-5;\)
\(2x=-5-1;\)
\(2x=-6;\)
\(x=-6:2;\)
\(x=-3.\)
|
Отже, рівняння має два корені: \(x_1=2;\) \(x_2=-3.\)
Відповідь: \(-3;\) \(2.\)