Щоб додати або відняти дроби, знаменниками яких є різні многочлени, необхідно:
- знайти спільний знаменник;
- звести дроби до спільного знаменника;
- виконати зазначені дії;
- за можливістю, спростити результат.
Якщо знаменниками дробів є многочлени, то спільним знаменником цих дробів також буде многочлен, який знаходимо так:
-
знаменники всіх дробів розкладаємо на множники (якщо це необхідно та можливо);
-
з одного знаменника беремо всі множники, а з інших тільки ті, яких немає в першому знаменнику (тобто ті, яких «бракує»).
Якщо многочлени в знаменниках дробів неможливо розкласти на множники, то спільний знаменник таких дробів дорівнює добутку знаменників усіх дробів.
Щоб безпомилково визначити додаткові множники для кожного дробу, треба отриманий спільний знаменник одразу записати в знаменнику «нового» дробу.
Щоб безпомилково визначити додаткові множники для кожного дробу, треба отриманий спільний знаменник одразу записати в знаменнику «нового» дробу.
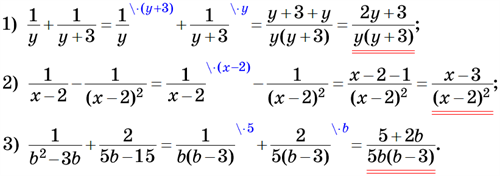
Приклад:
Додай дроби: .
Розв’язання
1. Знаменники дробів розкладаємо на множники:
2. Знаходимо спільний знаменник.
У знаменника першого дробу \(x(x-y)\), у порівнянні із знаменником другого дробу \(y(x-y)\), не вистачає множника \(y\), тому спільним знаменником цих дробів є многочлен .
3. Зводимо дроби до спільного знаменника, додаємо їх і спрощуємо результат:
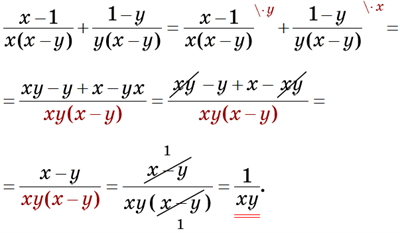
Спільний знаменник = (знаменник дробу) · (додатковий множник)