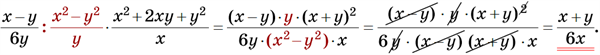Ми розглянули, як виконуються різні дії з раціональними дробами: додавання, віднімання, множення, ділення та піднесення до степеня. Але у всіх цих випадках ми виконували лише одну з арифметичних дій.
Тепер розглянемо спрощення складніших раціональних виразів, тобто виразів, у яких потрібно виконати декілька різних арифметичних дій із раціональними дробами, наприклад:
— множення та ділення дробів;
— множення та віднімання дробів;
— піднесення до степеня та додавання дробів.
Щоб правильно спростити такі вирази, необхідно:
-
дотримуватися порядку виконання арифметичних дій;
-
дотримуватися правил виконання цих дій;
-
пам'ятати, що всі дії виконуються тільки для тих значень змінних, за яких дріб має зміст.
Приклад:
Виконай дії: .
Розв’язання: це завдання можна виконати двома способами.
Перший спосіб
Спрощення виконується у дві дії: спочатку — ділення, а потім — множення. Чисельники і знаменники дробів розкладаються на множники під час виконання кожної дії.
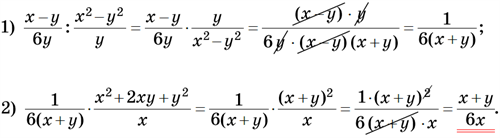
Другий спосіб
Дії ділення та множення виконуються одночасно. Чисельники і знаменники всіх дробів записуються одним дробом, а потім розкладаються на множники.