При розв'язанні нерівностей використовують такі правила:
1. Будь-який член нерівності можна перенести з однієї частини
нерівності в іншу з протилежним знаком, при цьому знак нерівності не змінюється.
нерівності в іншу з протилежним знаком, при цьому знак нерівності не змінюється.
2. Обидві частини нерівності можна помножити або поділити на одне
і те ж додатне число, не змінивши при цьому знак нерівності.
і те ж додатне число, не змінивши при цьому знак нерівності.
3. Обидві частини нерівності можна помножити або поділити на одне
й те саме від'ємне число, змінивши при цьому знак нерівності на
протилежний.
й те саме від'ємне число, змінивши при цьому знак нерівності на
протилежний.
Приклад:
Розв'язати нерівність .
Розв'язання.
Розв'язання.
1. Перенесемо член \(-3x\) в ліву частину нерівності, а член \(11\) — в праву частину нерівності, при цьому замінимо знаки на протилежні у \(-3x\) і у \(11\).
Тоді, отримаємо:
Тоді, отримаємо:
2. Поділимо обидві частини нерівності на від'ємне число \(-5\), при цьому знак нерівності \(<\), поміняється на \(>\), тобто ми перейдемо до нерівності протилежного змісту.
Отримаємо:
\(x >3\) — розв'язок заданої нерівності.
Зверни увагу!
Для запису розв'язку можна використовувати два варіанти: \(x>3\) або у вигляді числового проміжку.
Позначимо множину розв'язків нерівності на числовій прямій і запишемо відповідь у вигляді числового проміжку.
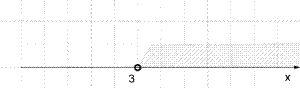
Відповідь: \(x >3\) або