Раціональною нерівністю з однією змінною \(x\) називають нерівність виду \(f(x)<g(x)\), де \(f(x)\) і \(g(x)\) — раціональні вирази, тобто алгебраїчні вирази, складені з чисел, змінної \(x\) і за допомогою математичних дій, тобто операцій додавання, віднімання, множення, ділення і піднесення до натурального степеня.
При розв'язанні раціональних нерівностей застосовують правила, які використовуються при розв'язанні лінійних і квадратних нерівностей.
За допомогою рівносильних перетворень раціональну нерівність зводять до вигляду \(h(x)<0\), де \(h(x)\) — алгебраїчний дріб або многочлен і застосовують метод інтервалів.
Приклад:
Розв'язати нерівність.
Розв'язання.
1. Знайдемо корені квадратного тричлена
і розкладемо його на множники за формулою
і розкладемо його на множники за формулою
2. Поділимо обидві частини нерівності на додатний при всіх значеннях \(x\)
вираз , при цьому знак нерівності \(>\) не зміниться.
вираз , при цьому знак нерівності \(>\) не зміниться.
3.Позначимо на числовій прямій корені і знайдемо знаки квадратного тричлена на кожному інтервалі.
Для цього з кожного інтервалу достатньо взяти по одному значенню і підставити замість \(x\) у тричлен.
Для цього з кожного інтервалу достатньо взяти по одному значенню і підставити замість \(x\) у тричлен.
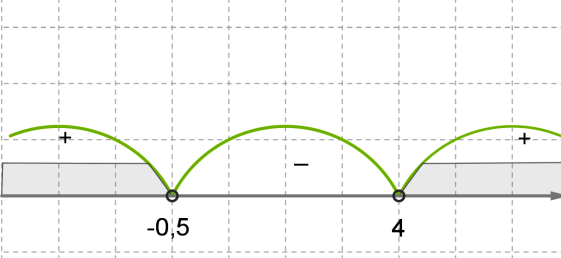
На інтервалі візьмемо \(x=-2\), тоді
На інтервалі візьмемо \(x=0\), тоді
На інтервалі візьмемо \(x=5\), тоді
Квадратний тричлен приймає додатні значення на інтервалах і .
Відповідь: