Якщо функція задана формулою виду ,
де — змінна, а — числа, що не дорівнюють одне одному,
числа які є нулями функції, тоді в кожному з проміжків, на які область визначення розбивається нулями функції, знак функції зберігається, а при переході через нуль її знак змінюється.
числа які є нулями функції, тоді в кожному з проміжків, на які область визначення розбивається нулями функції, знак функції зберігається, а при переході через нуль її знак змінюється.
Ця властивість використовується для розв'язання нерівностей.
Приклад:
Розв'язати нерівність
Знайдемо нулі функції.
Прирівняємо до нуля ліву частину і розв'яжемо рівняння, пам'ятаючи, що
добуток дорівнює нулю, коли хоча б один із множників дорівнює нулю.
Позначимо на координатній прямій нулі функції і знайдемо знаки функції на кожному проміжку.
Досить знати, який знак має функція в одному з цих проміжків, і, користуючись властивістю чергування знаків, визначити знаки у всіх інших проміжках.
Досить знати, який знак має функція в одному з цих проміжків, і, користуючись властивістю чергування знаків, визначити знаки у всіх інших проміжках.
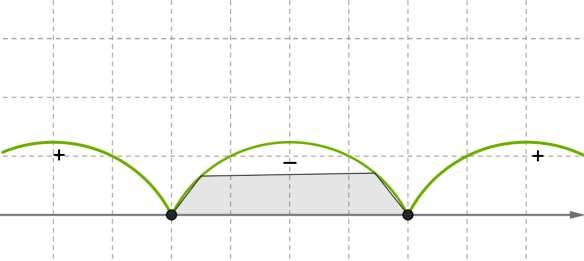
\(-\)2 5 \(x\)
На інтервалі візьмемо \(x=0\), тоді \(<0\)
На двох інших проміжках функція приймає додатні значення.
Розв'язати дану нерівність — це означає відповісти на запитання, за яких значень функція приймає від'ємні значення, отже, розв'язком нерівності є множина значень з проміжку .
Відповідь: .