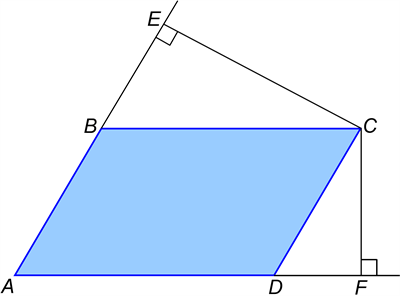
Висотою паралелограма називають перпендикуляр, проведений з будь-якої точки прямої, яка містить сторону паралелограма, до прямої, що містить протилежну сторону.
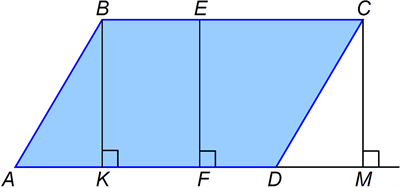
На малюнку \(BK\), \(EF\), \(CM\) — висоти паралелограма: \(BK\perp{AD}\), \(BK\perp{BC}\), \(EF\perp{AD}\), \(EF\perp{BC}\), \(CM\perp{AD}\), \(CM\perp{BC}\).
Оскільки \(AD\parallel{BC}\) і \(BK\perp{AD}\), \(BK\perp{BC}\), то довжина відрізка \(BK\) — відстань між сторонами \(AD\) і \(BC\) паралелограма.
Довжини відрізків \(EF\) і \(CM\) — також відстані між сторонами \(AD\) і \(BC\) паралелограма.
Отже, \(EF=CM=BK\).
Відстань між сторонами \(AB\) і \(CD\) визначається аналогічно.
Зверни увагу!
Із кожної вершини паралелограма можна провести дві висоти.
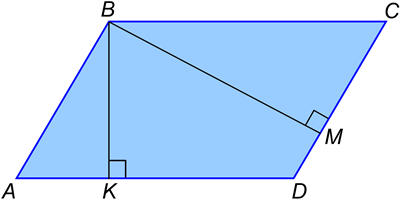
На малюнку із вершини \(B\) паралелограма проведено дві висоти \(BK\) і \(BM\), тобто \(BK\perp{AD}\), \(BM\perp{DC}\).
Також можна провести дві висоти й з вершини гострого кута паралелограма, наприклад, з вершини \(C\) — висоти \(CE\) і \(CF\), тобто \(CE\perp{AB}\), \(CF\perp{AD}\):