Чотирикутник, у якого протилежні сторони попарно паралельні, називають паралелограмом.
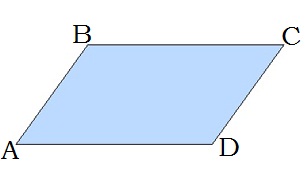
Властивості паралелограма:
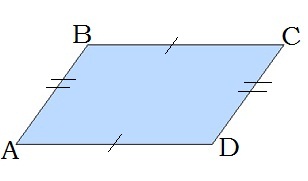
\(1.\) У паралелограмі протилежні сторони рівні.
\(AB = DC,\) \(BC = AD\)
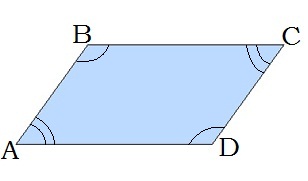
\(2.\) У паралелограмі протилежні кути рівні.
\( \angle{A}\ = \angle{C}\), \( \angle{B}\ = \angle{D}\)
\(3.\) Паралелограм є опуклим чотирикутником.
\(4.\) Діагоналі паралелограма точкою перетину діляться навпіл:
\(BO = OD,\) \(AO = OC\)
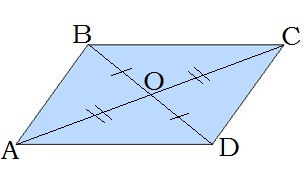
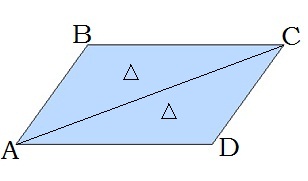
\(5.\) Діагональ паралелограма ділить його на два рівні трикутники:
\(\bigtriangleup{ABC}\ = \bigtriangleup{CDA}\)
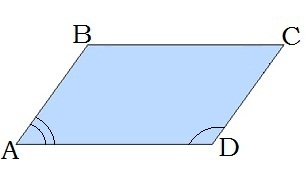
\(6.\) Сума будь-яких двох сусідніх кутів паралелограма дорівнює \(180^\circ\).
\( \angle{A}\ + \angle{D} \ = 180^\circ\)
\(7.\) Периметр паралелограма