Задача 1. Обчислити значення виразу
\(\dfrac{a + 2b}{a - 3b}\), де \(a, b\) – довільні числа.
Створимо математичну модель для цієї задачі:
вхідні дані: два довільних числа \(a\) і \(b\);
кінцеві результати: значення виразу \(z\);
формули: \(z = \dfrac{a + 2b}{a - 3b}\), якщо \(a - 3b \ne 0\), або «Вираз значення не має: ділення на нуль», якщо \(a - 3b = 0\).
Блок-схему алгоритму розв’язування цієї задачі наведено на малюнку 1.
\(\dfrac{a + 2b}{a - 3b}\), де \(a, b\) – довільні числа.
Створимо математичну модель для цієї задачі:
вхідні дані: два довільних числа \(a\) і \(b\);
кінцеві результати: значення виразу \(z\);
формули: \(z = \dfrac{a + 2b}{a - 3b}\), якщо \(a - 3b \ne 0\), або «Вираз значення не має: ділення на нуль», якщо \(a - 3b = 0\).
Блок-схему алгоритму розв’язування цієї задачі наведено на малюнку 1.
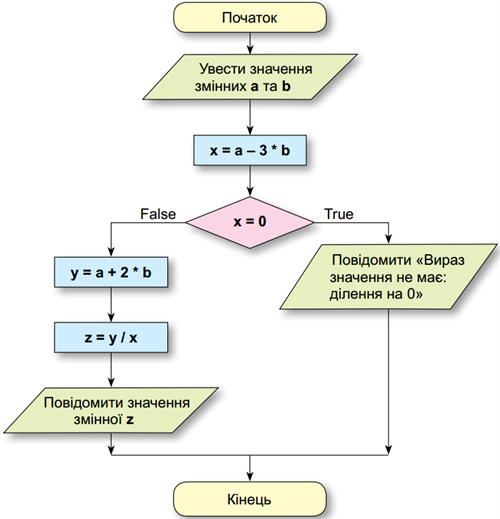

Рис.1
Розмістимо у вікні два поля для введення значень вхідних даних, підпишемо їх у відповідних написах, і кнопку, після вибору якої відбуватимуться відповідні обчислення. Результат виводитимемо у вікно повідомлень.
Текст проєкту буде такий:
from tkinter import*
from tkinter.messagebox import*
def click():
a = float(entry1.get())
b = float(entry2.get())
x = a - 3 * b
if x == 0:
showinfo(‘Результат’, ’Вираз значення не має: ділення на нуль’)
else:
y = a + 2 * b
z = y / x
showinfo(‘Результат’, str(z))
root = Tk()
root.geometry(‘300x250’)
label1 = Label(text = ‘Значення a’)
label1.pack(pady = 20)
entry1 = Entry()
entry1.pack()
entry1.focus_set()
label2 = Label(text = ‘Значення b’)
label2.pack(pady = 20)
entry2 = Entry()
entry2.pack()
button = Button(text = ‘Обчислити’, command = click)
button.pack(pady = 30)
 |
 |
|
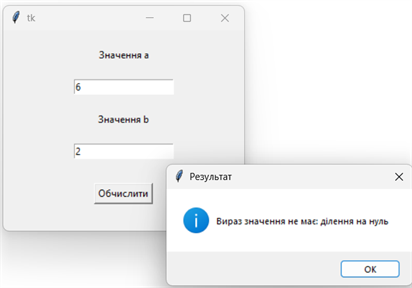
Результат виконання проєкту
при a = 6, b = 2
|
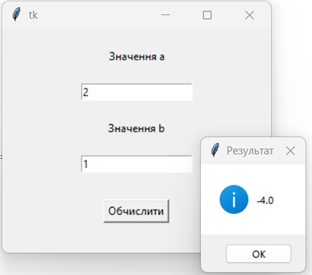
Результат виконання проєкту
при a = 2, b = 1
|
Задача 2. Обчислити значення функції
\(y =
\begin{cases}
2x - 12, & \text{якщо } x < -3 \text{ або } x > 5, \\
7 - 8x, & \text{для всіх інших } x.
\end{cases}\)
Математична модель:
вхідні дані: довільне число \(x\);
кінцеві результати: значення функції \(y\);
формули: якщо \(x < -3\) або \(x > 5\), то \(y = 2x - 12\), інакше \(y = 7 - 8x\).
\(y =
\begin{cases}
2x - 12, & \text{якщо } x < -3 \text{ або } x > 5, \\
7 - 8x, & \text{для всіх інших } x.
\end{cases}\)
Математична модель:
вхідні дані: довільне число \(x\);
кінцеві результати: значення функції \(y\);
формули: якщо \(x < -3\) або \(x > 5\), то \(y = 2x - 12\), інакше \(y = 7 - 8x\).
Розмістимо у вікні два поля: одне для введення значень вхідного даного, друге – для виведення значення кінцевого результату, підпишемо їх у відповідних написах, і кнопку, після вибору якої відбуватимуться відповідні обчислення.
Текст проєкту буде такий:
from tkinter import*
def click():
x = float(entry1.get())
if x < -3 or x > 5: y = 2 * x - 12
else: y = 7 - 8 * x
entry2.delete(0, END)
entry2.insert(0, str(y))
root = Tk()
label1 = Label(text = ‘Значення х’, font='Arial 14')
label1.pack(pady = 10)
entry1 = Entry(font='Arial 14')
entry1.pack()
entry1.focus_set()
label2 = Label(text = ‘Значення у’, font='Arial 14')
label2.pack(pady = 10)
entry2 = Entry(font='Arial 14')
entry2.pack()
button = Button(text = ‘Обчислити значення функції’, command = click, font='Arial 14')
button.pack(pady = 20)
Результати виконання проєкту при х = –4; х = 0; х = 7:
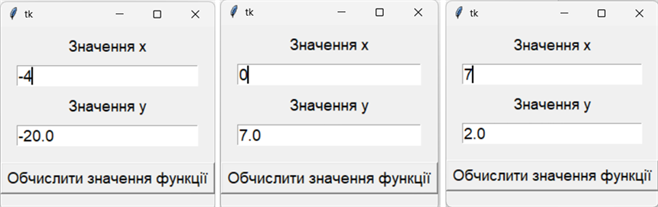

Джерела:
Інформатика : підруч. для 8 кл. закл. заг. серед.освіти / Йосиф Ривкінд [та ін.]. — Київ : Генеза, 2025.
Інформатика : підруч. для 8 кл. закл. заг. серед.освіти / О. О. Бондаренко, В. В. Ластовецький, О. П. Пилипчук, Є. А. Шестопалов. — Х. : Вид-во «Ранок», 2025.