На товарах ми можемо часто бачити надписи

Що вони означають?
Якщо ціле поділити на сто рівних частин і взяти одну таку частину, то отримаємо частину, тобто одну частину від ста. Позначають одну соту частину — \(1%\) (один відсоток або один процент).
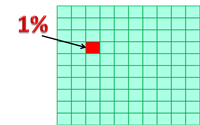
Відсоток — це одна сота частина

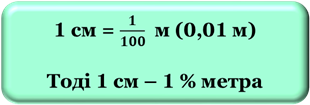
Приклад:
Задача № \(1\)
У колекції \(1200\) старовинних монет. Скільки монет припадає на один відсоток?
Розв'язання.
Нехай \(1200\) монет — це \(100\ \)%. Тоді на \(1\) % припадає: \(1200 : 100 = 12\) (монет).
Отже \(1\) % — це \(12\) монет.
Задача № \(2\)
На свята в магазині продали \(34000\) валентинок. Скільки святкових листівок припадає на \(1\) %.
Розв'язання.
Загальна кількість валентинок, \(34000\) — це \(100\) %. Тоді на \(1\) % припадає: \(34000 : 100 = 340\ \)(листівок).
Маємо: \(1\) % — \(це\ 340\) листівок.
Задача № \(3\)
За роботу у святкові дні йде подвійна оплата. Леся працювала у вихідні, яку оплату вона отримає у відсотках?
Розв'язання.
Якщо оплата праці за договором — \(100\) %, тоді подвійна оплата — це . Тоді Леся отримає \(200\) % суми описаної у договорі.
Якщо відома величина \(1\)%, то можна знайти ціле, помноживши на \(100\).
Приклад:
Задача № \(4\)
У понеділок було \(45\) відвідувачів у зоопарку, що становить \(1\) % всіх відвідувачів за місяць. Скільки відвідувачів у зоопарку за місяць.
Розв'язування
Якщо \(1\) % — це \(45\) гостей, тоді за місяць відвідувачів буде
відвідувачів.
Відповідь: \(4500\) відвідувачів за місяць.
Зверни увагу!
Відсотки, звичайні дроби і десяткові дроби можуть відображати однакові частини, тому, для зручності, при розв'язуванні задач можна переводити відсотки у дроби, а дроби у відсотки.
