1. Задачі, які приводять до поняття похідної

Задача 1 (швидкість руху). По прямій, на якій задані початок відліку, одиниця виміру (метр) і напрям, рухається деяке тіло (матеріальна точка). Закон руху задане формулою $s=s(t)$, де $t$ - час (у секундах), $s(t)$ - положення тіла на прямій (координата рухомої матеріальної точки) в момент часу $t$ по відношенню до початку відліку (в метрах). Знайти швидкість руху тіла в момент часу $t$ (в $м/с$).

Розв'язання . Припустимо, що в момент часу $t$ тіло перебувало в точці $M$.

1 uzd..bmp

Дамо аргументу $t$ приріст $Δ t$ і розглянемо ситуацію в момент часу $t + Δ t$ . Координата матеріальної точки стане іншою, тіло в цей момент буде знаходитися в точці $P : OP = s (t + Δ t)$ .

Отже, за $Δ t$ секунд тіло перемістилося з точки $M$ в точку $P$. Маємо: $MP = OP - OM = s (t + Δ t) - s (t)$ . Отриману різницю ми назвали приростом функції: $s (t + Δ t) - s (t) = Δ s$ . Тож, $MP = Δ s (м)$ . Неважко знайти середню швидкість $v_{ср}$ руху тіла за проміжок часу $[t; t + Δ t]$ : $v_{ср} = \frac{Δ s}{Δ t}$ $(м/с)$.

А що таке швидкість $v(t)$ в момент часу $t$ (її називають миттєвою швидкістю)? Можна сказати так: це середня швидкість руху за проміжок часу $[t; t + Δ t]$ за умови, що $Δ t$ обирається все менше і менше; точніше: за умови, що $Δ t \to 0$ . Це означає, що $v (t) = \lim_{Δ t \to 0} v_{ср}$ .

Отже,

v = \lim_{Δ t \to 0} \frac{Δ s}{Δ t}

Задача 2 (дотична до графіка функції). Дан графік функції $y=f(x)$. На ньому обрана точка $M (a; f(a))$, в цій точці до графіка функції проведена дотична (ми припускаємо, що вона існує). Знайти кутовий коефіцієнт дотичної.

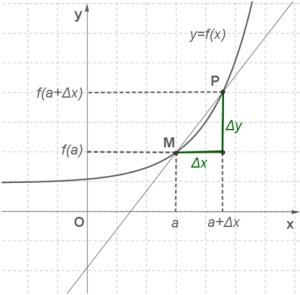
2.uzd.05.T.bmp

Розв'язання. Дамо аргументу приріст $Δ x$ і розглянемо на графіку точку $P$ з абсцисою $a + Δ x$ . Ордината точки $P$ дорівнює $f (a + Δ x)$ . Кутовий коефіцієнт січної $MP$, тобто тангенс кута між січною і віссю $x$, обчислюється за формулою $k_{січ} = \frac{Δ y}{Δ x}$ .

Якщо ми тепер спрямуємо $Δ x$ до нуля, тоді точка $P$ почне наближатися по кривій до точки $M$. Дотичну ми охарактеризували, як граничне положення січної при цьому наближенні. Отже, можна вважати, що кутовий коефіцієнт дотичної $k_{дот} = \lim_{Δ x \to 0} k_{січ}$ буде обчислюватися за формулою $k_{дот} = \lim_{Δ x \to 0} k_{січ}$ . Використовуючи наведену вище формулу для $k_{січ}$ , отримуємо:

$k_{дот} = \lim_{Δ x \to 0} \frac{Δ y}{Δ x}$

Попередня тема

Повернутись до теми

Наступна теорія

Відправити відгук

Знайшли помилку?

Розкажіть нам!

1. Задачі, які приводять до поняття похідної

Теорія: