Границя відношення приросту функції до приросту аргумента, якщо приріст аргументу наближається до нуля (і ця границя існує), називається похідною цієї функції.
(іноді замість пишеться .)
Отже, .
Приклад:
1)
2)
Фізичний (механічний) зміст похідної полягає в наступному. Якщо \(s(t)\) - закон прямолінійного руху тіла, тоді похідна виражає миттєву швидкість в момент часу \(t\):
.
Геометричний зміст похідної полягає в наступному. Якщо до графіка функції \(y=f(x)\) в точці з абсцисою \(x=a\) можна провести дотичну, яка не паралельна осі \(y\), тоді виражає кутовий коефіцієнт дотичної:
.
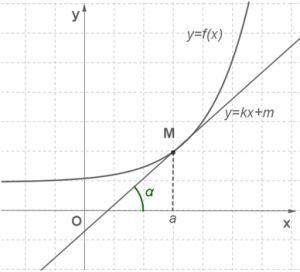
Оскільки , тоді правильна рівність .
Алгоритм знаходження похідної для функції \(y=f(x)\)
1. Зафіксувати значення \(x\), знайти \(f(x)\).
2. Дати аргументу \(x\) приріст , перейти в нову точку , знайти .
3. Знайти приріст функції: .
4. Додати відношення .
5. Обчислити . Ця границя і є .
