Графік функції \(y=\sqrt{x}\) можна використовувати під час розв’язування рівнянь та систем рівнянь графічним способом.
Приклад:
Розв’яжи графічно рівняння \(2\sqrt{x}=8-x.\)
Розв’язання
Оскільки ми поки що не вміємо будувати графік функції \(y=2\sqrt{x},\) то поділимо обидві частини рівняння на число \(2.\)
Одержимо рівняння \(\sqrt{x}=4-0,5x.\)
Побудуємо графіки функцій \(f(x)=\sqrt{x}\) і \(g(x)=4-0,5x\) в одній системі координат.
Графіком функції \(f(x)=\sqrt{x}\) є гілка гіперболи, а графіком функції \(g(x)=4-0,5x\) є пряма:
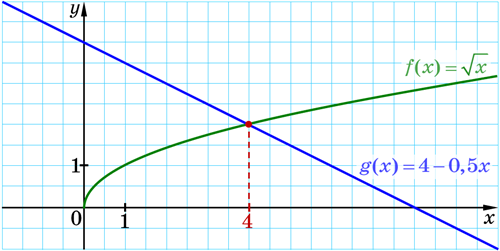
Графіки перетинаються в точці з абсцисою \(4\).
Перевіркою переконуємося, що число \(4\) — корінь рівняння.
Справді, \(2\sqrt{4}=2·2=4\) і \(8-4=4.\)
Відповідь: \(4.\)
Приклад:
Розв’яжи графічно систему рівнянь \(\begin{cases} y=\sqrt{x}, \\ y=0,25x+0,75. \end{cases}\)
Розв’язання
Побудуємо графіки функцій \(y=\sqrt{x}\) і \(y=0,25x+0,75\) в одній системі координат.
Графіком функції \(y=\sqrt{x}\) є гілка гіперболи, а графіком функції \(y=0,25x+0,75\) є пряма:
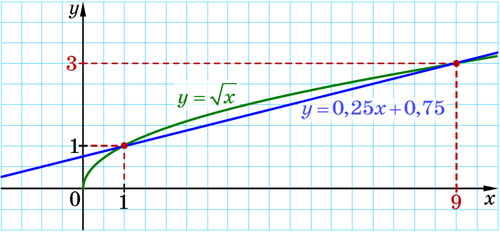
Графіки перетинаються в точках з координатами \((1;1)\) і \((9;3)\).
Перевіркою переконуємося, що пари чисел \((1;1)\) і \((9;3)\) — розв’язки заданої системи рівнянь.
Справді, \(1=\sqrt{1}\) і \(1=0,25·1+0,75;\) \(3=\sqrt{9}\) і \(3=0,25·9+0,75.\)
Відповідь: \((1;1);\) \((9;3).\)
Справді, \(1=\sqrt{1}\) і \(1=0,25·1+0,75;\) \(3=\sqrt{9}\) і \(3=0,25·9+0,75.\)
Відповідь: \((1;1);\) \((9;3).\)