Сформулюємо деякі властивості функції \(y=\sqrt{x}\).
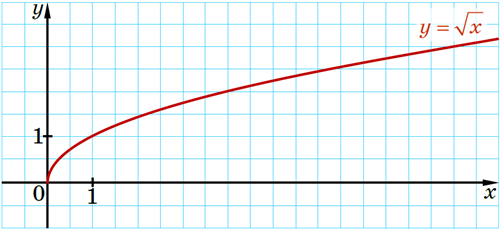
Властивості функції \(y=\sqrt{x}\)
| Область визначення функції | Множина всіх невід’ємних чисел, тобто \(x\geqslant{0}\) |
| Область значень функції | Множина всіх невід’ємних чисел, тобто \(y\geqslant{0}\) |
| Графік функції | Гілка параболи, що виходить з точки \((0;0),\) усі інші точки графіка лежать у першій координатній чверті |
| Нулі функції | Має один нуль при \(x=0\) |
| Монотонність функції | Функція зростає на всій області визначення, тобто більшому значенню аргументу відповідає більше значення функції |
Остання властивість дає можливість порівнювати значення виразів, що містять квадратні корені.
Приклад:
Порівняй числа \(\sqrt{15}\) і \(\sqrt{14}.\)
Розв’язання
Оскільки \(15>14,\) то \(\sqrt{15}>\sqrt{14}.\)
Відповідь: \(\sqrt{15}>\sqrt{14}.\)
Приклад:
Порівняй числа \(8\) і \(\sqrt{65}.\)
Розв’язання
Оскільки \(8=\sqrt{64},\) а \(64<65,\) тому \(\sqrt{64}<\sqrt{65},\) отже, \(8<\sqrt{65}.\)
Відповідь: \(8<\sqrt{65}.\)
Розв’язання
Оскільки \(8=\sqrt{64},\) а \(64<65,\) тому \(\sqrt{64}<\sqrt{65},\) отже, \(8<\sqrt{65}.\)
Відповідь: \(8<\sqrt{65}.\)
Приклад:
Порівняй числа \(5\sqrt{2}\) і \(4\sqrt{3}.\)
Розв’язання
Розв’язання
Внесемо множник в обох виразах під знак кореня:
\(5\sqrt{2}=\sqrt{25}·\sqrt{2}=\sqrt{25·2}=\sqrt{50};\)
\(4\sqrt{3}=\sqrt{16}·\sqrt{3}=\sqrt{16·3}=\sqrt{48}.\)
Оскільки \(50>48,\) то \(\sqrt{50}>\sqrt{48},\) а тому \(5\sqrt{2}>4\sqrt{3}.\)
Відповідь: \(5\sqrt{2}>4\sqrt{3}.\)
Відповідь: \(5\sqrt{2}>4\sqrt{3}.\)