Нехай маємо квадрат, площа якого становить \(S\) см², а довжина його сторони дорівнює \(a\) см.
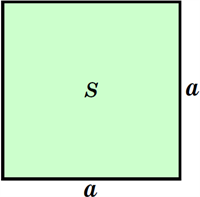
Оскільки \(S=a^2,\) то залежність довжини сторони \(a\) квадрата від його площі \(S\) можна задати формулою:
| \(a=\sqrt{S}\) |
Побудуємо графік цієї функції.
Оскільки ми поки що не знаємо, як виглядє графік функції \(y=\sqrt{x},\) то складемо таблицю значень цієї функції для кількох значень аргументу.
Для цього надамо незалежній змінній \(x\) декілька конкретних значень та обчислимо за формулою \(y=\sqrt{x}\) відповідні значення залежної змінної \(y\):
| \(x\) | \(0\) | \(0,25\) | \(1\) | \(2,25\) | \(4\) | \(6,25\) | \(9\) |
| \(y\) | \(0\) | \(0,5\) | \(1\) | \(1,5\) | \(2\) | \(2,5\) | \(3\) |
Позначимо ці точки на координатній площині.
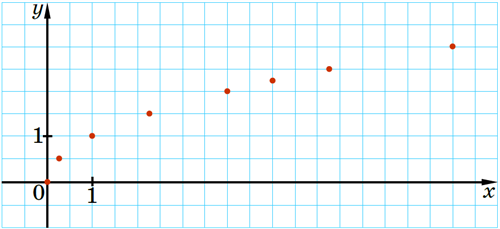
Чим більше точок, координати яких задовольняють рівняння \(y=\sqrt{x}\), ми позначимо, тим менше отримана фігура відрізнятиметься від графіка функції \(y=\sqrt{x}\):
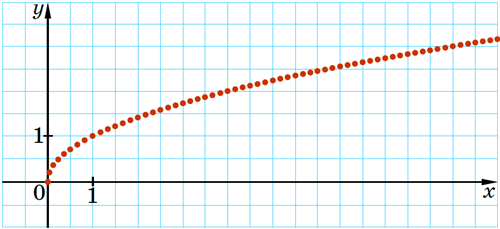
Тому, сполучивши ці точки плавною лінією, отримуємо графік функції \(y=\sqrt{x}\):
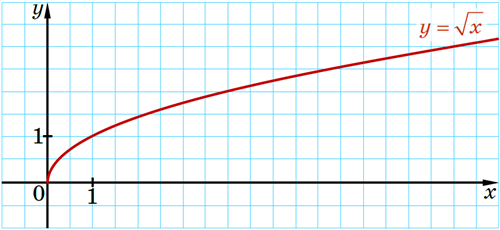
Фігуру, яка є графіком функції \(y=\sqrt{x}\), називають гілкою параболи.
Приклад:
Побудуй графік функції
\(y(x)=\begin{cases} -3x, \> \color{Black}{\textsf{якщо}} \> x<0, \\ \\ \sqrt{x}, \> \color{Black}{\textsf{якщо}} \> 0\leqslant{x}\leqslant{4}, \\ \\ \dfrac{8}{x}, \> \color{Black}{\textsf{якщо}} \> x>4. \end{cases}\)
Розв’язання
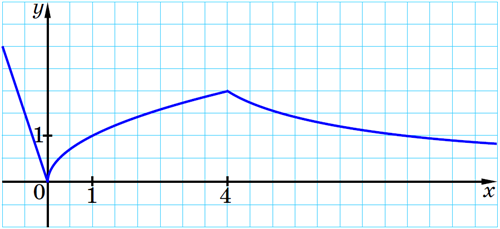
Для \(x<0\) графіком заданої функції є частина графіка функції \(y=-3x\) — частина прямої.
Для \(0\leqslant{x}\leqslant{4}\) графіком заданої функції є частина графіка функції \(y=\sqrt{x}\) — частина гілки параболи.
Для \(x>4\) графіком заданої функції є частина графіка функції \(y=\dfrac{8}{x}\) — частина гіперболи.
Відповідь: графік зображено на рисунку.