Нехай маємо квадрат зі стороною \(x\).
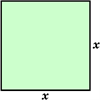
Позначимо площу цього квадрата через \(y\). Тоді \(y=x^2\).
Якщо змінювати сторону квадрата \(x\), то буде змінюватися і його площа \(y\).
Зрозуміло, що кожному значенню змінної \(x\) відповідає єдине значення змінної \(y\). Отже, залежність змінної \(y\) від змінної \(x\) є функціональною, а формула \(y=x^2\) задає функцію.
Оскільки у виразі \(x^2\) допустимими значеннями змінної \(x\) є всі числа, то областю визначення функції \(y=x^2\) також є всі числа.
Побудуємо графік функції \(y=x^2\).
Оскільки ми поки що не знаємо, як виглядє графік функції \(y=x^2\), то складемо таблицю значень цієї функції для кількох значень аргументу.
Для цього надамо незалежній змінній \(x\) декілька конкретних значень та обчислимо за формулою \(y=x^2\) відповідні значення залежної змінної \(y\):
якщо \(x=-3\), то \(y=(-3)^2=9\);
якщо \(x=-2,5\), то \(y=(-2,5)^2=6,25\);
якщо \(x=-2\), то \(y=(-2)^2=4\);
якщо \(x=-1,5\), то \(y=(-1,5)^2=2,25\);
якщо \(x=-1\), то \(y=(-1)^2=1\);
якщо \(x=-0,5\), то \(y=(-0,5)^2=0,25\);
якщо \(x=0\), то \(y=0^2=0\);
якщо \(x=0,5\), то \(y=0,5^2=0,25\);
якщо \(x=1\), то \(y=1^2=1\);
якщо \(x=1,5\), то \(y=1,5^2=2,25\);
якщо \(x=2\), то \(y=2^2=4\);
якщо \(x=2,5\), то \(y=2,5^2=6,25\);
якщо \(x=3\), то \(y=3^2=9\).
Маємо таблицю:
| \(x\) | \(-3\) | \(-2,5\) | \(-2\) | \(-1,5\) | \(-1\) | \(-0,5\) | \(0\) |
| \(y\) | \(9\) | \(6,25\) | \(4\) | \(2,25\) | \(1\) | \(0,25\) | \(0\) |
| \(x\) | \(0,5\) | \(1\) | \(1,5\) | \(2\) | \(2,5\) | \(3\) |
| \(y\) | \(0,25\) | \(1\) | \(2,25\) | \(4\) | \(6,25\) | \(9\) |
Позначимо на координатній площині точки, координати \((x; y)\) яких наведено в таблиці:
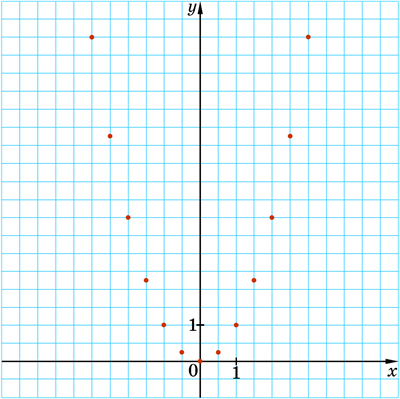
Чим більше точок, координати яких задовольняють рівняння \(y=x^2\), ми позначимо, тим менше отримана фігура відрізнятиметься від графіка функції \(y=x^2\):
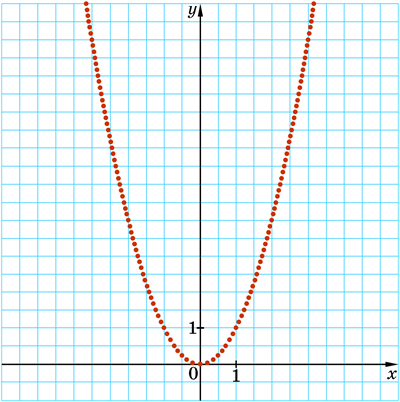
Тому, сполучивши ці точки плавною лінією, отримуємо графік функції \(y=x^2\):
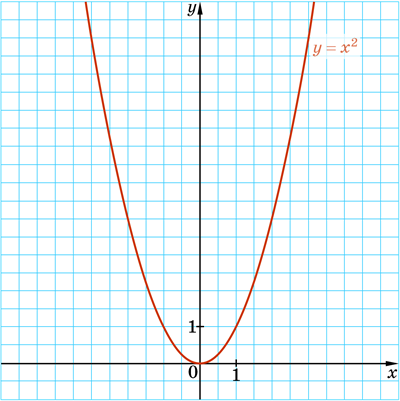
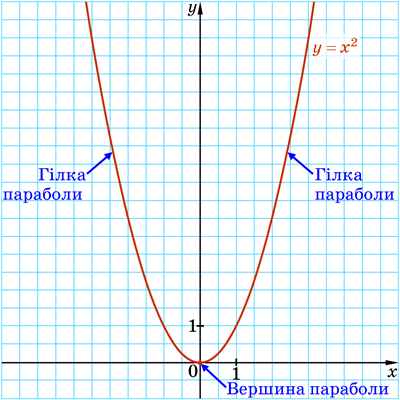
Фігуру, яка є графіком функції \(y=x^2\), називають параболою.
Точку \((0;0)\) називають вершиною параболи.
Вершина ділить параболу на дві частини, кожну з яких називають гілкою параболи.