Сформулюємо деякі властивості функції \(y=x^2\).
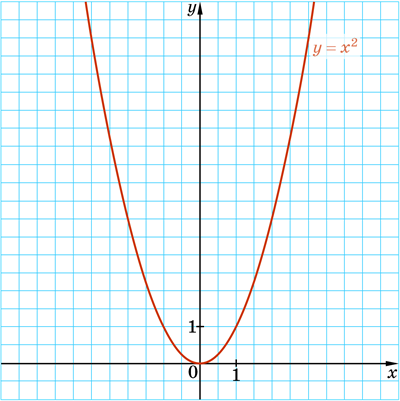
Оскільки ніяких обмежень на змінну \(x\) немає (ми поки що знаємо одне обмеження — не можна ділити на \(0\), а тут не відбувається ділення на змінну або на вираз зі змінною), то областю визначення функції \(y=x^2\) є всі числа.
Пара чисел \((0;0)\) є розв’язком рівняння \(y=x^2\). Отже, графік заданої функції проходить через початок координат. Звідси задана функція має один нуль: \(y=0\) при \(x=0\).
Оскільки \(y=x^2\) і \(x^2\ge{0}\), то \(y\ge{0}\), тобто графік функції не містить точок з від’ємними ординатами. Отже, областю значень функції \(y=x^2\) є всі невід’ємні числа.
Функція зростає, якщо зі збільшенням значення аргументу значення функції збільшується. Тобто функція \(y=x^2\) зростає, якщо \(x>0\).
Функція спадає, якщо зі збільшенням аргументу значення функції зменшується. Тобто функція \(y=x^2\) спадає, якщо \(x<0\).
Зверни увагу!
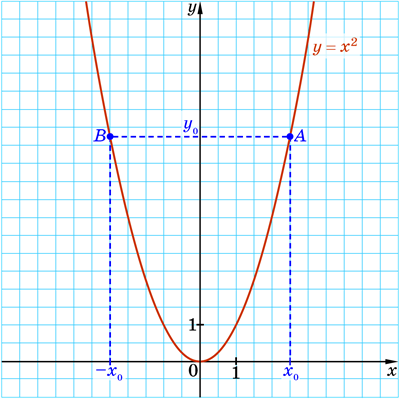
Коли є правильною рівність \(y_0=x_0^2\), то є правильною й рівність \(y_0=(-x_0)^2\). Тоді можна зробити такий висновок: якщо точка \(A(x_0;y_0)\) належить параболі \(y=x^2\), то точка \(B(-x_0;y_0)\) також належить цій параболі (див. малюнок).

Для зручності вивчені властивості функції \(y=x^2\) наведемо у таблиці.
Властивості функції \(y=x^2\)
| Область визначення | Усі числа |
| Область значень | Усі невід’ємні числа |
| Графік | Парабола з вершиною в точці \((0;0)\), гілки якої напрямлені вгору. Усі точки графіка, крім вершини параболи, лежать вище від осі абсцис |
| Нулі функції (значення аргументу, при якому значення функції дорівнює \(0\) | Має один нуль при \(x=0\) |
|
Функція зростає
|
Якщо \(x>0\)
|
|
Функція спадає
|
Якщо \(x<0\)
|
| Властивості графіка | Якщо точка \(A(x_0;y_0)\) належить параболі \(y=x^2\), то точка \(B(-x_0;y_0)\) також належить цій параболі |
