Приклад:
Розв’яжи графічно рівняння \(x^2=2x+3\).
Розв’язання
Графік функції \(y = x^2\) — парабола, а функції \(y = 2x + 3\) — пряма, що проходить через точки \((0; 3)\) і \((2; 7)\).
Побудуємо графіки цих функцій в одній системі координат (див. малюнок).
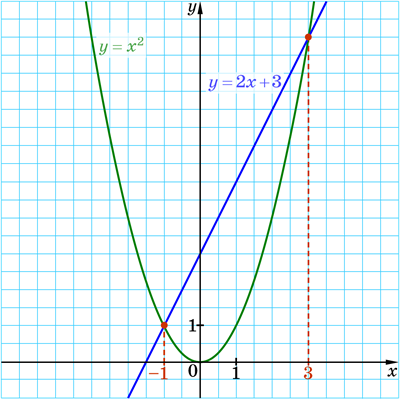
Вони перетинаються у двох точках, абсциси яких \(x = -1\) і \(x = 3\).
Оскільки графічний метод не завжди дає точні результати, то пересвідчимося, що числа \(–1\) і \(3\) дійсно є коренями рівняння:
1) якщо \(x = –1\), то \(x^2 = (–1)^2 = 1\) і \(2x + 3 = 2 · (–1) + 3 = -2 + 3 = 1\);
2) якщо \(x = 3\), то \(x^2 = 3^2 = 9\) і \(2x + 3 = 2 · 3 + 3 = 6 + 3 = 9\).
Отже, \(-1\) і \(3\) — корені рівняння \(x^2 = 2x + 3\).
Відповідь: \(–1; 3\).
Приклад:
Розв’яжи графічно рівняння \(\dfrac{8}{x}=x^2\).
Розв’язання
Графік функції \(y =\dfrac{8}{x}\) — гіпербола, а функції \(y = x^2\) — парабола.
Побудуємо графіки цих функцій в одній системі координат (див. малюнок).
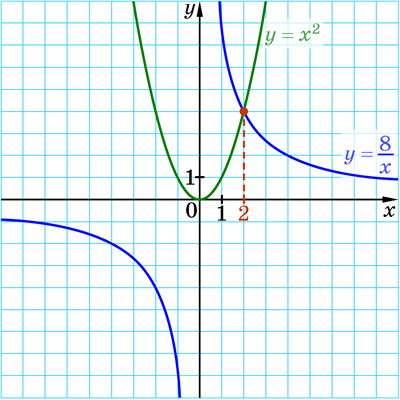
Графіки перетинаються в одній точці, абсциса якої \(x = 2\).
Оскільки графічний метод не завжди дає точні результати, то пересвідчимося, що число \(2\) дійсно є коренем рівняння: якщо \(x = 2\), то \(\dfrac{8}{x} = \dfrac{8}{2} = 4\) і \(x^2 = 2^2 = 4\).
Отже, \(2\) — корінь рівняння \(\dfrac{8}{x} = x^2\).
Відповідь: \(2\).
