Сума кутів чотирикутника дорівнює \(360^\circ\).
Розглянемо випадок, коли чотирикутник є опуклим.
Проведемо в чотирикутнику \(ABCD\) діагональ \(BD\), яка розіб'є його на два трикутники: \(\bigtriangleup{ABD}\) і \(\bigtriangleup{CBD}\).
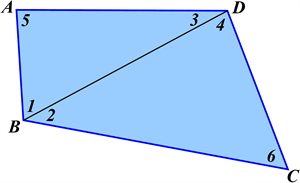
Тоді \(\angle{ABC}=\angle{1}+\angle{2}\), \(\angle{ADC}=\angle{3}+\angle{4}\), а сума кутів чотирикутника \(ABCD\) дорівнює:
\(\angle{A}+\angle{ABC}+\angle{C}+\angle{ADC}=\angle{5}+\angle{1}+\angle{2}+\angle{6}+\angle{3}+\angle{4}\).
Ураховуючи, що \(\angle{1}+\angle{3}+\angle{5}=180^\circ\) (як сума кутів \(\bigtriangleup{ABD}\)) та \(\angle{2}+\angle{4}+\angle{6}=180^\circ\) (як сума кутів \(\bigtriangleup{CBD}\)), знайдемо суму кутів чотирикутника \(ABCD\):
\(\angle{5}+\angle{1}+\angle{2}+\angle{6}+\angle{3}+\angle{4}=(\angle{1}+\angle{3}+\angle{5})+(\angle{2}+\angle{4}+\angle{6})=180^\circ + 180^\circ = 360^\circ\).
Аналогічно можна довести, що сума кутів неопуклого чотирикутника також дорівнює \(360^\circ\).
Отже, сума кутів чотирикутника дорівнює \(360^\circ\).
Приклад:
Знайди кути чотирикутника, якщо їхні градусні міри відносяться як \(1 : 2 : 10 : 5\). Опуклим чи неопуклим є цей чотирикутник?
Розв’язання
Нехай кути чотирикутника дорівнюють \(x\), \(2x\), \(10x\) і \(5x\).
За умовою задачі складаємо рівняння: \(x+2x+10x+5x=360\).
Розв’яжемо це рівняння:
\(18x=360;\)
\(x=360:18;\)
\(x=20.\)
Отже кути чотирикутника дорівнюють: \(20^\circ\); \(2·20^\circ=40^\circ\); \(10·20^\circ=200^\circ\); \(5·20^\circ=100^\circ\).
Оскільки один із кутів чотирикутника більший за \(180^\circ\), то цей чотирикутник — неопуклий.
Відповідь. \(20^\circ\); \(40^\circ\); \(200^\circ\); \(100^\circ\); неопуклий.
