Ромбом називають паралелограм, у якого всі сторони рівні.
Властивості ромба
Оскільки ромб є паралелограмом, то він має всі властивості паралелограма.
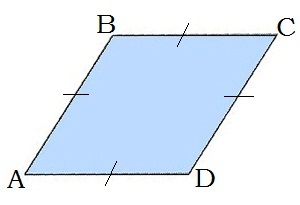
\(1.\) Протилежні сторони ромба рівні: \(AB = BC = CD = AD\) (оскільки всі сторони рівні).
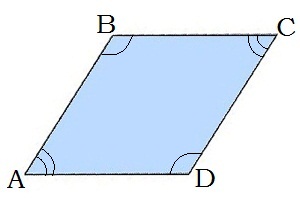
\(2.\) Протилежні кути ромба рівні: \( \angle{A}\ = \angle{C}\), \( \angle{B}\ = \angle{D}\).
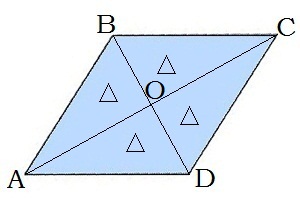
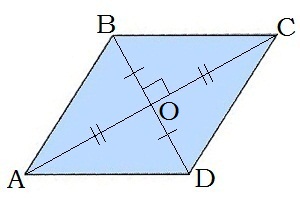
\(3.\) Діагоналі ромба точкою перетину діляться навпіл: \(BO = OD\), \(AO = OC\).
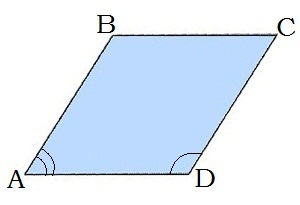
\(4.\) Сума кутів, прилеглих до однієї сторони ромба, дорівнює \(180^\circ\): \( \angle{A}\ + \angle{D} \ = 180^\circ\).
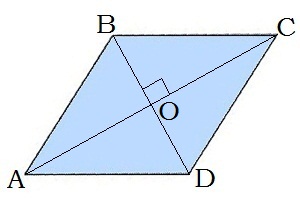
\(5.\) Діагоналі ромба взаємно перпендикулярні: \(AC\) \(BD\).
\(6.\) Діагоналі ромба є також бісектрисами його кутів (ділять кути ромба навпіл).
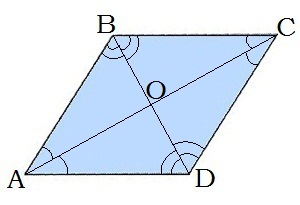
\(7.\) Діагоналі ділять ромб на чотири рівні прямокутні трикутники. Трикутники \(ABO,\) \(CBO,\) \(CDO,\) \(ADO\) — рівні прямокутні трикутники.