Прямокутником називають паралелограм, у якого всі кути прямі.

Властивості прямокутника
Оскільки прямокутник є паралелограмом, то він має всі властивості паралелограма.\(1.\) Протилежні сторони прямокутника рівні: \(AB = CD,\) \(BC = AD\).
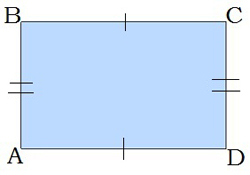
\(2.\) Кожен кут прямокутника дорівнює \(90\)\(^\circ\). Це означає, що протилежні кути рівні й сума кутів, прилеглих до однієї сторони, дорівнює \(180\)\(^\circ\).
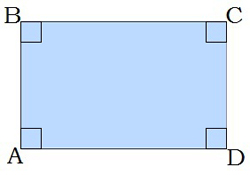
\(3.\) Діагоналі прямокутника точкою перетину діляться навпіл: \(BO = OD,\) \(AO = OC\). Крім того, \(BO = OD = AO = OC\) (див. шосту властивість).
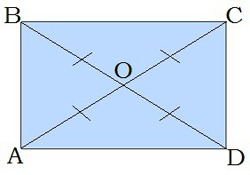
\(4.\) Діагональ прямокутника ділить його на два рівні прямокутні трикутники.
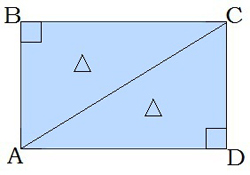
\(5.\) Різносторонні кути при діагоналі рівні.
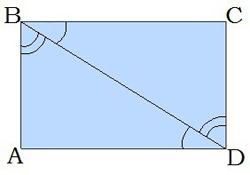
\(6.\) Діагоналі прямокутника рівні: \(BD = AC\).
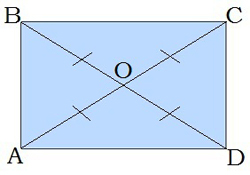
\(7.\) Точка перетину діагоналей прямокутника рівновіддалена від усіх його вершин.
\(8.\) Периметр прямокутника обчислюється за формулою: .
