Для двійкового кодування чисел їх переводять у двійкову систему числення. У звичній для нас десятковій системі числення для запису числа використовують цифри від \(0\) до \(9\), а у двійковій системі – лише цифри \(0\) та \(1\). Число \(10\) є основою десяткової системи числення, а число \(2\) – основою двійкової системи. Щоб зазначати основу системи числення в записі числа, використовують нижній індекс.
Як ви знаєте, цифри в десятковому записі числа (від останньої до першої) вказують, скільки одиниць, десятків, сотень, тисяч та інших степенів числа \(10\) міститься в заданому числі.
Наприклад:
\(5328_{10} = 5 \cdot 10^3 + 3 \cdot 10^2 + 2 \cdot 10^1 + 8 \cdot 10^0 = 5 \cdot 1000 + 3 \cdot 100 + 2 \cdot 10 + 8\)
У двійковому записі числа цифри вказують, скільки одиниць, двійок, четвірок, вісімок та інших степенів числа \(2\) міститься в заданому числі. Наприклад:
\(1011_{2} = 1 \cdot 2^3 + 0 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 2^0 = 1 \cdot 8 + 0 \cdot 4 + 1 \cdot 2 + 1\)
Якщо в останньому виразі виконати обчислення, то запис числа з двійкового можна перевести у десятковий:
\(1011_{2} = 1 \cdot 8 + 0 \cdot 4 + 1 \cdot 2 + 1 = 11_{10}\)
Відповідно можна перевести десятковий запис числа у двійковий, подавши число сумою степенів двійки:
\(13_{10} = 1 \cdot 2^3 + 1 \cdot 2^2 + 0 \cdot 2^1 + 1 \cdot 2^0 = 1101_{2}\)
Як ви знаєте, цифри в десятковому записі числа (від останньої до першої) вказують, скільки одиниць, десятків, сотень, тисяч та інших степенів числа \(10\) міститься в заданому числі.
Наприклад:
\(5328_{10} = 5 \cdot 10^3 + 3 \cdot 10^2 + 2 \cdot 10^1 + 8 \cdot 10^0 = 5 \cdot 1000 + 3 \cdot 100 + 2 \cdot 10 + 8\)
У двійковому записі числа цифри вказують, скільки одиниць, двійок, четвірок, вісімок та інших степенів числа \(2\) міститься в заданому числі. Наприклад:
\(1011_{2} = 1 \cdot 2^3 + 0 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 2^0 = 1 \cdot 8 + 0 \cdot 4 + 1 \cdot 2 + 1\)
Якщо в останньому виразі виконати обчислення, то запис числа з двійкового можна перевести у десятковий:
\(1011_{2} = 1 \cdot 8 + 0 \cdot 4 + 1 \cdot 2 + 1 = 11_{10}\)
Відповідно можна перевести десятковий запис числа у двійковий, подавши число сумою степенів двійки:
\(13_{10} = 1 \cdot 2^3 + 1 \cdot 2^2 + 0 \cdot 2^1 + 1 \cdot 2^0 = 1101_{2}\)
Алгоритм переведення десяткового числа в двійкову систему
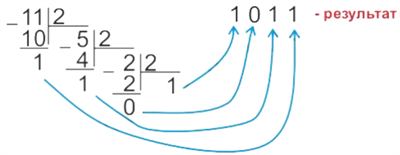
Для переведення десяткового числа в двійкову систему його необхідно послідовно ділити на 2 до тих пір, поки не залишиться залишок, менший або рівний 1. Число в двійковій системі записується як послідовність останнього результату ділення і залишків від ділення в зворотному порядку.
Приклад:
Перевести число \(11_{10}\) в двійкову систему числення.
\(11_{10} = 1011_{2}\)
\(11_{10} = 1011_{2}\)
Для переведення двійкового числа в десяткове необхідно його записати у вигляді многочлена, що складається з добутків цифр числа і відповідного степеня числа \(2\), і обчислити за правилами десяткової арифметики:
\(X_{2} = A_{n} \cdot 2^{n-1} + A_{n-1} \cdot 2^{n-2} + A_{n-2} \cdot 2^{n-3} + ... + A_{2} \cdot 2^{1} + A_{1} \cdot 2^{0}\)
\(X_{2} = A_{n} \cdot 2^{n-1} + A_{n-1} \cdot 2^{n-2} + A_{n-2} \cdot 2^{n-3} + ... + A_{2} \cdot 2^{1} + A_{1} \cdot 2^{0}\)
При переведенні зручно користуватися таблицею степенів двійки:

Приклад:
Число \(11101000_{2}\) перевести в десяткову систему числення.
\(11101000_{2} = 1 \cdot 2^7 + 1 \cdot 2^6 + 1 \cdot 2^5 + 0 \cdot 2^4 + 1 \cdot 2^3 + 0 \cdot 2^2 + 0 \cdot 2^1 + 0 \cdot 2^0 = 232_{10}\)
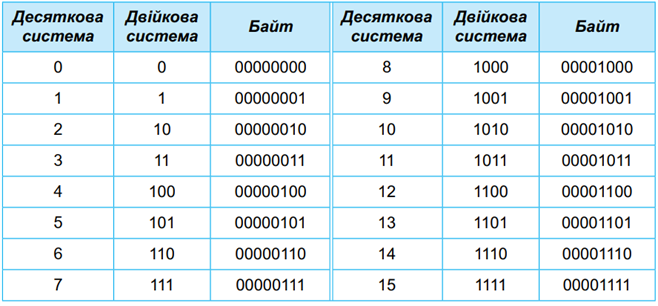
Якщо двійковий запис числа доповнити зліва нулями до отримання кількості цифр, кратної восьми, то отримаємо набір байтів, якими кодується число. Перші \(16\) цілих невід’ємних чисел, записані в десятковій і двійковій системах числення, та відповідні їм байти наведено у таблиці.
Джерела:
Інформатика : підруч. для 8-го кл. закл. заг. серед. освіти / Й. Ривкінд та ін. — Київ : Генеза, 2025
Інформатика : підруч. для 8 кл. закл. загал. серед. освіти / [О. О. Бондаренко, В. В. Ластовецький, О. П. Пилипчук, Є. А. Шестопалов]. — Харків : Вид-во «Ранок», 2025
https://komplogika.jimdofree.com/