Система числення — сукупність правил запису (зображення) чисел за допомогою символів (цифрових знаків) і виконання операцій над ними.
Непозиційні системи
У непозиційних системах числення кількісне значення цифри не залежить від її місця розташування в зображенні числа.
Приклад:
Давньоєгипетська десяткова система: кожен символ означає число 10 у певному степені..
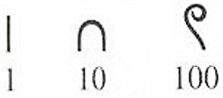
Число 345:

Приклад:
Римська система

XXXII=(X+X+X)+(I+I)=30+2=32
Якщо ліворуч від більшої цифри стоїть менша, то значення дорівнює різниці між більшою та меншою цифрами.
Обмеження:
-
перед L(50) і C(100) може стояти лише X(10);
-
перед D(500) і M(1000) — тільки C(100);
-
перед V(5) — тільки I(1).
Число 444 у римській системі обчислення буде записано у вигляді
CDXLIV = (D-C)+(L-X)+(V-I) = 400+40+4=444.
Позиційні системи
У позиційних системах числення кількісне значення цифри залежить не лише від значення самої цифри, а й від її місця (позиції) у записі числа. Основні характеристики:
Основа системи числення (\(q\)) — кількість цифр, що можна використовувати.
Наприклад:
- у десятковій \((q=10)\): \(0-9\);
- у двійковій \((q=2)\): \(0\) і \(1\);
- у шістнадцятковій \((q=16)\): \(0-9\) і \(A-F\).
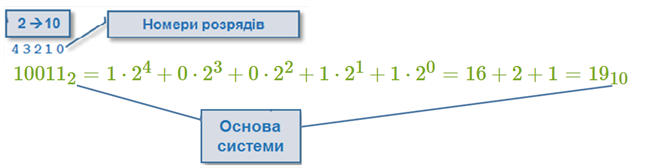
Вага розряду = \(q^n\), де \(n\) — номер розряду, тобто вага розрядів у позиційних системах числення найчастіше дорівнює основі системи числення у степені номера розряду.
Щоб визначити кількісне значення цифри в позиційній системі числення, необхідно помножити цю цифру на основу системи в степені того номера розряду, в якому розміщена ця цифра.
Число \(245_{10}\):
\(2 \cdot 10^2 + 4 \cdot 10^1 + 5 \cdot 10^0 = 200 + 40 + 5\)
\(2 \cdot 10^2 + 4 \cdot 10^1 + 5 \cdot 10^0 = 200 + 40 + 5\)
Переведення десяткового числа у шістнадцяткове
Перевести число \(254_{10}\) у шістнадцяткову систему.
Розв’язання:
Метод ділення з остачею:
\(254 : 16 = 15\), остача \(14 \rightarrow E\)
\(15 : 16 = 0\), остача \(15 \rightarrow F\)
Читаємо знизу вгору \(\rightarrow FE_{16}\).
Відповідь: \(FE_{16}\)
Розв’язання:
Метод ділення з остачею:
\(254 : 16 = 15\), остача \(14 \rightarrow E\)
\(15 : 16 = 0\), остача \(15 \rightarrow F\)
Читаємо знизу вгору \(\rightarrow FE_{16}\).
Відповідь: \(FE_{16}\)
Переведення шістнадцяткового числа у десяткове
Розв’язання:
\(1A_{16} = 1 \cdot 16^1 + A \cdot 16^0\)
\(A = 10 \rightarrow 1 \cdot 16 + 10 \cdot 1 = 16 + 10 = 26\)
Відповідь: \(1A_{16} = 26_{10}\)