На координатній площині можна будувати графіки залежностей між різними величинами.
Графік залежності температури від часу
Наприклад, метеорологи упродовж доби вимірюють температуру повітря через кожні дві години. Результати занесли до таблиці:
| t,год | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 23 | 24 |
| T,°C | 4 | 2 | 0 | -3 | -4 | -1 | 2 | 5 | 7 | 5 | 4 | 3 | 2 | 1 |
Ця таблиця характеризує залежність температури повітря від часу. Таку залежність можна подати графічно, на прямокутній системі координат. На осі абсцис відкладемо значення часу (t, год) так, що одній клітинці відповідатиме одна година. На осі ординат задамо — (T, °C) так, що одній клітинці відповідатиме один градус.
Таким чином, абсциса кожної точки — значення часу, а ордината — значення температури на цей час.
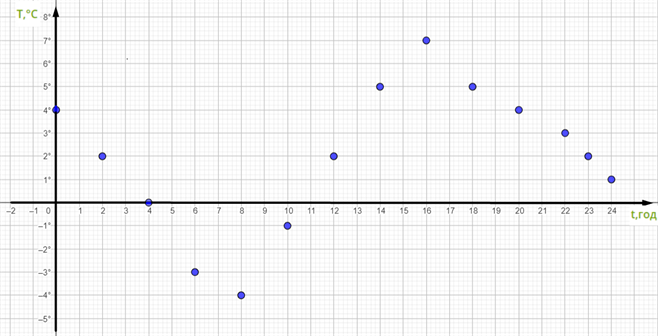
Якщо припустити, що різких стрибків температури не було, сполучивши отримані точки плавною лінією, одержимо графік залежності температури повітря від часу впродовж доби.
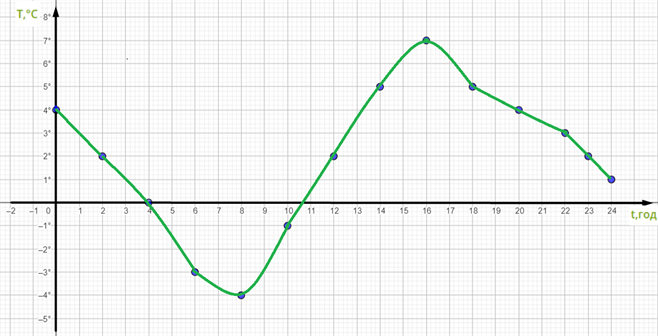
За допомогою графіка можна дати відповіді на багато питань (яке значення температури було найвище, коли значення були однаковими, та ін.).
Графік залежності відстані від часу
Розглянемо приклад руху мотоцикліста зі швидкістю 40 км/год. При підрахунку залежності відстані (s, км) від часу (t, год) було одержано таблицю:
| t, год | 0 | 1 | 2 | 3 | 4 | 5 |
| s, км | 0 | 40 | 80 | 120 | 160 | 200 |
Побудуємо графік цього руху. На осі абсцис відкладаємо значення часу (t, год) так, що одній годині відповідає одна клітинка, а на осі ординат відкладемо значення відстані (s, км) так, що одній клітинці відповідатиме 20 км.
Сполучивши точки відрізками, одержимо графік залежності відстані від часу за сталої швидкості.
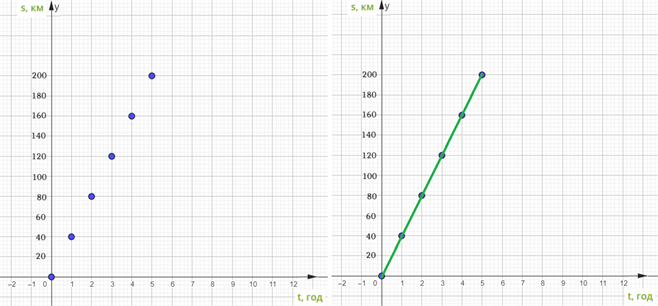
Усі точки графіка руху лежать на одній прямій. Також, залежність \(s\) від \(t\) можна задати формулою \(s=40t\).
Зверни увагу!
Усі точки графіка залежності прямо пропорційних величин лежать на одній прямій.
Графік руху є прямою (або її частиною), тому такий графік можна побудувати за будь-якими двома його точками.
Джерела:
О. Істер. Математика. Підручник для 6 класу закладів загальної середньої освіти (у 2-х частинах). Частина 2. — Київ. "Генеза".—2023.
Математика. Підручник для 6 класу закладів загальної середньої освіти (у 2-х частинах). Частина 2. Тарасенкова Н., Богатирьова І. та ін. — Київ. "Оріон". — 2023.
