Координатний промінь із додатними числами доповнимо протилежним йому променем і нанесемо на нього такі ж поділки. Отримаємо координатну пряму.
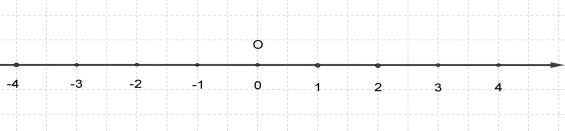
Координатна пряма — це пряма із вказаними на ній початком відліку \(O\) (\(0\)), напрямом і одиничним відрізком.
Точка \(O\) (\(0\)) — початок відліку. Праворуч від неї позначають додатні числа, а ліворуч — від'ємні. Стрілочка показує додатний напрям відліку на координатній прямій.
Біля стрілочки часто ставлять букву x, y, z або іншу букву латинського алфавіту. У таких випадках говорять: «вісь x», «вісь y», «вісь z» відповідно.
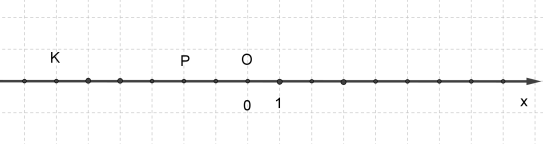
На координатній прямій важливе розміщення точок.
Зверни увагу!
Кажуть: «Точка \(P\) розміщена ліворуч від точки \(O\)».
«Точка \(P\) розміщена праворуч від точки \(K\)».
Число, що показує розташування точки на прямій, називається координатою точки.
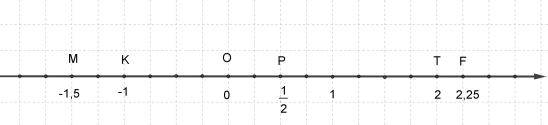
Зверни увагу!
Одиничний відрізок може бути різним на координатних прямих.
У даному випадку одиничний відрізок дорівнює \(4\) клітинкам та одній клітинці відповідає \(0,25\) одиничного відрізка.
У даному випадку одиничний відрізок дорівнює \(4\) клітинкам та одній клітинці відповідає \(0,25\) одиничного відрізка.
Запишемо координати точок \(M, K, P, T, F\):
Зверни увагу!
Замість слів «позначимо точку з координатою, що дорівнює...» коротко говорять «позначимо число...».
Будь які дві точки \(A\) і \(B\) називають симетричними відносно точки \(O\), якщо точка \(O\) —
середина відрізка \(AB\). Точку \(O\) — називають центром симетрії. На координатній прямій симетричні точки \(A\) і \(B\) знаходяться відносно точки \(O\) на однаковій відстані та відрізняються лише знаками.
Приклад:
Точки \(A(-12)\) і \(B(12)\) — симетричні відносно точки \(O\).